Paso 4: Perforar los agujeros triangulares

En esta sección vamos a ver en cómo generar un patrón de prismas de las caras de la esfera geodésica, que vamos luego a restar de nuestra bola del paso 2 para generar los orificios reales.
Primero necesitamos crear prismas de los triángulos de la esfera geodésica.
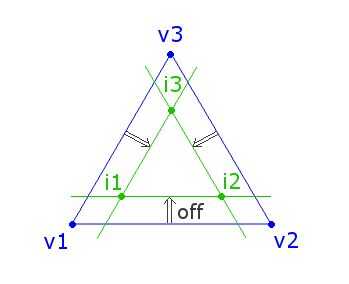
Para ello, primero creamos un triángulo más pequeño dentro de cada triángulo de la geodésica
esfera por compensación de los bordes hacia adentro por una distancia fija e informática
los puntos de intersección de los bordes traducidos que conforman los vértices
del nuevo triángulo (véase el cuadro arriba).
Para generar el prisma, utilicé el método solidFromSlicespara extrudir el triángulo corriente (i1 i2 i3) ortogonalmente a su superficie.
La función createPrism
// generates a prism from a unit sphere triangle, a radius, and an offset function createPrism(sphereTri, radius, offset) {// compute the coordinates of the vertices of the input triangle var v1 = new CSG.Vector3D(scalar_mul(sphereTri[0], radius)); var v2 = new CSG.Vector3D(scalar_mul(sphereTri[1], radius)); var v3 = new CSG.Vector3D(scalar_mul(sphereTri[2], radius)); // make plane base (v1, x, y) var xAxis = v2.minus(v1).unit(); var v13 = v3.minus(v1); var yAxis = v13.minus(xAxis.times(v13.dot(xAxis))).unit(); // retrieve 2d coordinates of the triangle vertices in that base var v1_2d = new CSG.Vector2D(0, 0); var v2_2d = new CSG.Vector2D(v2.minus(v1).dot(xAxis), 0); var v3_2d = new CSG.Vector2D(v3.minus(v1).dot(xAxis), v3.minus(v1).dot(yAxis)); // get the middle of each segment in the plane var v12_2d = v2_2d.minus(v1_2d); var v23_2d = v3_2d.minus(v2_2d); var v31_2d = v1_2d.minus(v3_2d); // get unit vector perpendicular to i1i2 segment in the plane var ortho12 = new CSG.Vector2D(-v12_2d.y, v12_2d.x).unit(); if(v3_2d.minus(v1_2d).dot(ortho12) <0) ortho12 = ortho12.times(-1); var ortho23 = new CSG.Vector2D(-v23_2d.y, v23_2d.x).unit(); if(v1_2d.minus(v2_2d).dot(ortho23) <0) ortho23 = ortho23.times(-1); var ortho31 = new CSG.Vector2D(-v31_2d.y, v31_2d.x).unit(); if(v2_2d.minus(v1_2d).dot(ortho31) <0) ortho31 = ortho31.times(-1); // translate all tri segments inward by the same offset var s12b = translate_segment([v1_2d, v2_2d], ortho12.times(offset)); var s23b = translate_segment([v2_2d, v3_2d], ortho23.times(offset)); var s31b = translate_segment([v3_2d, v1_2d], ortho31.times(offset)); // compute intersection points of translated segments in the plane var i1 = intersect(s12b, s23b); var i2 = intersect(s23b, s31b); var i3 = intersect(s31b, s12b); var i1_3d = v1.plus(xAxis.times(i1.x)).plus(yAxis.times(i1.y)); var i2_3d = v1.plus(xAxis.times(i2.x)).plus(yAxis.times(i2.y)); var i3_3d = v1.plus(xAxis.times(i3.x)).plus(yAxis.times(i3.y)); // create a polygon from the intersection points var tri = new CSG.Polygon([ new CSG.Vertex(i1_3d), new CSG.Vertex(i2_3d), new CSG.Vertex(i3_3d) ]); var zAxis = tri.plane.normal; return tri.solidFromSlices({ numslices: 2, // amount of slices loop: false, // final CSG is closed by looping (start = end) like a torus callback: function(t,slice) { // echo("t:" + t) return this.translate( scalar_mul([zAxis.x, zAxis.y, zAxis.z], 4*t) ); } }).translate(scalar_mul([zAxis.x, zAxis.y, zAxis.z], -2)); } // multiplies a 3d vector by a scalar function scalar_mul(v, c) { return [c*v[0], c*v[1], c*v[2]]; } // translates a 2d segment by a 2d vector function translate_segment(seg, vec) { s0b = seg[0].plus(vec); s1b = seg[1].plus(vec); return [s0b, s1b]; } // computes the intersection of 2 2d segments function intersect(s1, s2) { var p = s1[0]; var q = s2[0]; var r = s1[1].minus(p); var s = s2[1].minus(q); var u = q.minus(p).cross(r)/r.cross(s); var t = q.minus(p).cross(s)/r.cross(s); if(r.cross(s) != 0 && u >= 0 && u<= 1 && t >= 0 && t<= 1) return p.plus(r.times(t)); return null; } Haciendo uso de la función de createPrism sobre, donde ahora puede generar todo el
patrón de agujero por iteración de los triángulos de la esfera geodésica:
Secuencia del patrón de agujero
function main(){ var ballDiameter = 40; // mm var segmentWidth = 2; // mm var sphereTris = []; // holds list of geodesic sphere triangles addPolyCb = function(v1, v2, v3) { sphereTris.push([ [v1.x, v1.y, v1.z], [v2.x, v2.y, v2.z], [v3.x, v3.y, v3.z] ]); } createGeodesicSphere(addPolyCb, 1); var holePattern; for(j=0; j!=sphereTris.length; ++j) { var prism = createPrism(sphereTris[j], ballDiameter/2., segmentWidth/2.); if(j==0) { holePattern = prism; } else holePattern = holePattern.union(prism); } return holePattern; } function subdivide(v1, v2, v3, addPolyCb, depth) { if(depth == 0) { addPolyCb(v1, v2, v3); return; } var v12 = v1.plus(v2).unit(); var v23 = v2.plus(v3).unit(); var v31 = v3.plus(v1).unit(); var newDepth = depth - 1; subdivide(v1, v12, v31, addPolyCb, newDepth); subdivide(v2, v23, v12, addPolyCb, newDepth); subdivide(v3, v31, v23, addPolyCb, newDepth); subdivide(v12, v23, v31, addPolyCb, newDepth); } function createGeodesicSphere(addPolyCb, depth) { var X = 0.525731112119133606; var Z = 0.850650808352039932; var vdata = [ [-X, 0.0, Z], [ X, 0.0, Z ], [ -X, 0.0, -Z ], [ X, 0.0, -Z ], [ 0.0, Z, X ], [ 0.0, Z, -X ], [ 0.0, -Z, X ], [ 0.0, -Z, -X ], [ Z, X, 0.0 ], [ -Z, X, 0.0 ], [ Z, -X, 0.0 ], [ -Z, -X, 0.0 ] ]; var tindices = [ [0, 4, 1], [ 0, 9, 4 ], [ 9, 5, 4 ], [ 4, 5, 8 ], [ 4, 8, 1 ], [ 8, 10, 1 ], [ 8, 3, 10 ], [ 5, 3, 8 ], [ 5, 2, 3 ], [ 2, 7, 3 ], [ 7, 10, 3 ], [ 7, 6, 10 ], [ 7, 11, 6 ], [ 11, 0, 6 ], [ 0, 1, 6 ], [ 6, 1, 10 ], [ 9, 0, 11 ], [ 9, 11, 2 ], [ 9, 2, 5 ], [ 7, 2, 11 ] ]; for(var i = 0; i < 20; i++) subdivide( new CSG.Vector3D(vdata[tindices[i][0]]), new CSG.Vector3D(vdata[tindices[i][1]]), new CSG.Vector3D(vdata[tindices[i][2]]), addPolyCb, depth); }













