Paso 1: El acelerómetro

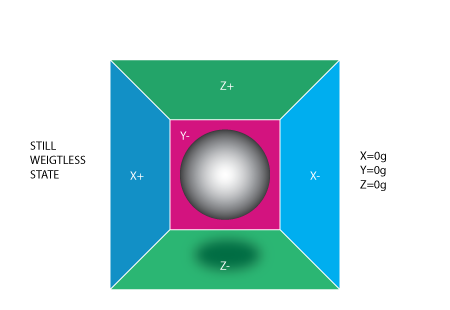
Si tenemos esta caja en un lugar con ningún campo de gravitación o de hecho con no otros campos que podrían afectar la posición de la bola - la bola simplemente flotará en el medio de la caja. Se puede imaginar el cuadro está en el espacio exterior lejos lejos lejos de los cuerpos cósmicos, o si un lugar es difícil de encontrar, imaginar por lo menos una nave espacial en órbita alrededor del planeta donde todo está en estado de ingravidez. De la foto de arriba vemos que asignamos a cada eje un par de paredes (quitamos la pared Y + por lo que podemos ver dentro de la caja). Imagina que cada pared es sensible a la presión. Si pasamos de repente la caja a la izquierda (acelera con aceleración 1g = 9.8 m/s ^ 2), la bola golpeará la pared X-. Luego medir la fuerza de presión que la bola se aplica a la pared y un valor de-1 g en el eje X.
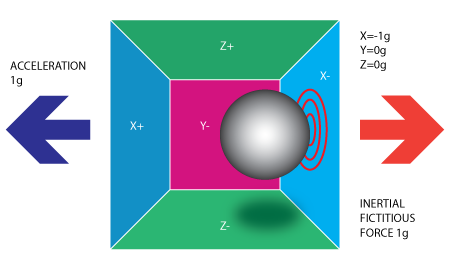
Tenga en cuenta que el acelerómetro realmente detecta una fuerza que está dirigida en la dirección opuesta al vector aceleración. Esta fuerza se denomina fuerza inercial o ficticia de la fuerza . Una cosa que debes aprender de esto es que un acelerómetro mide aceleración indirectamente a través de una fuerza que se aplica a una de sus paredes (según nuestro modelo, puede ser un muelle o algo más en los acelerómetros de la vida real). Esta fuerza puede ser causada por la aceleración, pero como veremos en el siguiente ejemplo no es siempre causada por la aceleración.
Si tomamos nuestro modelo y ponerlo en la tierra la bola caerá en la pared de Z y aplica una fuerza de 1g en la pared de fondo, como se muestra en la siguiente imagen:
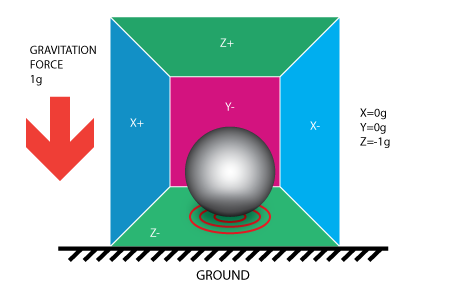
En este caso no es mover la caja pero todavía obtenemos una lectura de g-1 en el eje Z. La presión que la bola ha aplicado en la pared fue causada por una fuerza de gravitación. En teoría sería un tipo diferente de la fuerza - por ejemplo, si usted se imagina que nuestra bola es metálica, colocar un imán al lado de la caja podría mover la pelota para que caiga otro muro. Esto fue dicho para probar que en esencia medidas acelerómetro fuerza no aceleración. Sólo ocurre que aceleración provoca una fuerza inercial que es capturada por el mecanismo de detección de la fuerza del acelerómetro.
Mientras que este modelo no es exactamente cómo se construye un sensor de MEMS es a menudo útil en la solución de acelerómetro problemas relacionados. Hay sensores realmente similares metálicos bolas dentro, se llaman interruptores de inclinación, sin embargo, son más primitivos y generalmente puede decir sólo si el aparato está inclinado dentro de algunas de la gama o no, no el grado de inclinación.
Hasta ahora hemos analizado el acelerometro en un solo eje de salida y esto es todo lo que obtendrá con acelerómetros de un solo eje. El valor real de acelerómetros triaxiales viene del hecho de que puede detectar fuerzas inerciales en las tres hachas. Volvamos a nuestro modelo de caja y vamos a girar los caja 45 grados a la derecha. La bola tocará 2 paredes ahora: z y X como se muestra en la siguiente imagen:
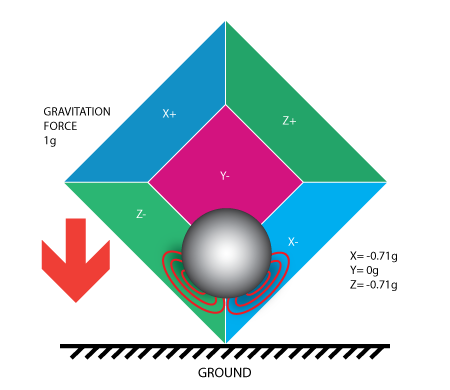
Los valores de 0.71 no son arbitrarios, son en realidad una aproximación para SQRT(1/2). Esto quedará más claro como presentamos nuestro siguiente modelo para el acelerómetro.
En el modelo anterior hemos fijado la fuerza de gravitación y girar nuestro cuadro imaginario. En los últimos 2 ejemplos hemos analizado la salida en 2 posiciones diferentes de la caja, mientras que el vector fuerza se mantuvo constante. Mientras que esto era útil en la comprensión de cómo interactúa el acelerómetro con fuerzas externas, es más práctico realizar cálculos si arreglar el sistema de coordenadas a los ejes del acelerómetro y imagine que el vector de fuerza gira alrededor de nosotros.
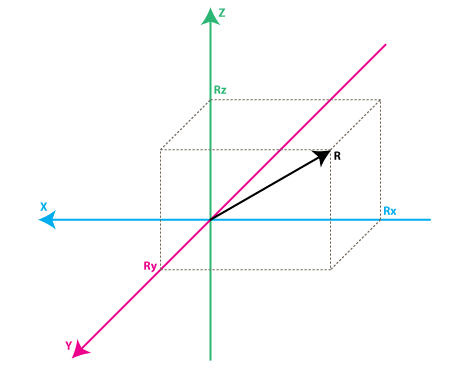
Echa un vistazo en el modelo anterior, conserva los colores de los ejes para que pueda hacer una transición mental desde el modelo anterior al nuevo. Imagínense que cada eje en el nuevo modelo es perpendicular a las caras respectivas de la caja en el modelo anterior. El vector R es el vector de fuerza que mide el acelerómetro (podría ser la fuerza de gravedad o la fuerza inercial de los ejemplos anteriores o una combinación de ambos). RX, Ry, Rz son proyección del vector R en X, Y, Z ejes. Tenga en cuenta a la siguiente relación:
R ^ 2 = Rx ^ 2 + Ry ^ 2 + Rz ^ 2 (EC. 1)
que es básicamente el equivalente del Teorema de Pitágoras en 3D.
Recuerde que un poco antes te dije que los valores de SQRT(1/2) ~ 0.71 no son al azar. Si enchufa en la fórmula anterior, después de haber recordado que nuestra fuerza de gravitación fue 1 g podemos comprobar:
1 ^ 2 = (-SQRT(1/2)) ^ 2 + 0 ^ 2 + (-SQRT(1/2)) ^ 2
simplemente sustituyendo R = 1, Rx = - SQRT(1/2), Ry = 0, Rz =-SQRT(1/2) en Eq.1
Después de un largo preámbulo de teoría estamos más cercanos de acelerómetros de la vida real. Los valores de Rx, Ry, Rz son realmente relacionada linealmente con los valores que la salida de su acelerómetro de vida real y que pueden utilizar para realizar varios cálculos.
Antes de llegar allí vamos a hablar un poco sobre la manera de acelerómetros entregará esta información a nosotros. Acelerómetros más caerá en dos categorías: digitales y analógicos. Acelerómetros digitales le dará información utilizando un protocolo serial como I2C, SPI y USART, mientras que los acelerómetros análogos generará un nivel de voltaje dentro de un rango predefinido que se tiene que convertir en un valor digital mediante un módulo de ADC (analógico al convertidor digital). No entraré en mucho detalle acerca de cómo funciona ADC, en parte porque es un tema tan extenso y en parte porque es diferente de una plataforma a otra. Algunos microcontrolador tendrá un módulos ADC incorporados algunos de ellos necesitan componentes externos para realizar las conversiones del ADC. No importa qué tipo de ADC módulo utilizas te termina con un valor en un cierto rango. Para módulo de ejemplo un ADC de 10 bits a la salida un valor en el rango de 0..1023, tenga en cuenta que 1023 = 2 ^ 10 -1. Un módulo de ADC de 12 bits a un valor en el rango de 0..4095 de la salida, nota que 4095 = 2 ^ 12-1.
Vamos a pasar por considerar un ejemplo sencillo, supongamos que nuestro módulo de 10 bits ADC nos dio los siguientes valores para los tres canales del acelerómetro (ejes):
AdcRx = 586
AdcRy = 630
AdcRz = 561
Cada módulo ADC tiene una tensión de referencia, supongamos que en nuestro ejemplo es 3, 3V. Para convertir un valor de adc de 10 bits a voltaje utilizamos la siguiente fórmula:
VoltsRx = AdcRx * Vref / 1023
Una nota rápida aquí: que para 8 bits ADC el último divisor sería 255 = 2 ^ 8-1 y por último divisor de 12 bits ADC sería 4095 = 2 ^ 12 -1.
Aplicando esta fórmula a todos los 3 canales obtenemos:
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (que ronda todos los resultados a 2 decimales)
VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V
VoltsRz = 561 * 3.3V / 1023 = ~ 1.81V
Cada acelerómetro tiene un nivel de voltaje de zero-g, usted puede encontrar en especificaciones, esto es la tensión que corresponde a 0g. Para obtener un valor de voltaje firmado tenemos que calcular el cambio de este nivel. Supongamos que nuestro nivel de tensión de 0g es VzeroG = 1. 65V. Calculamos la tensión cambia de puesto de zero-g voltaje como sigue::
DeltaVoltsRx = 1.89V - 0.24V = 1. 65V
DeltaVoltsRy = 2.03V - 0.38V = 1. 65V
DeltaVoltsRz = 1.81V - 0.16V = 1. 65V
Ahora tenemos nuestras lecturas del acelerómetro en voltios, todavía no está en g (9,8 m/s ^ 2), para hacer la final conversión aplicamos la sensibilidad del acelerómetro, normalmente expresada en mV/g. permite decir nuestra sensibilidad = 478.5mV / g = 0.4785V / valores de sensibilidad de g. pueden encontrarse en las especificaciones del acelerómetro. Para obtener los valores de fuerza final expresados en g, utilizamos la siguiente fórmula:
RX = DeltaVoltsRx / sensibilidad
RX = 0.24V / 0.4785V / g = ~ 0.5 g
Ry = 0.38V / 0.4785V / g = ~ 0,79 g
RZ = 0.16V / 0.4785V / g = ~ 0,33 g
Por supuesto podríamos combinar todos los pasos de una fórmula, pero pasé por todos los pasos para aclarar cómo vas de lecturas ADC a un componente del vector de fuerza expresado en g.
RX = (AdcRx * Vref / 1023 - VzeroG) / sensibilidad (EC.2)
Ry = (AdcRy * Vref / 1023 - VzeroG) / sensibilidad
RZ = (AdcRz * Vref / 1023 - VzeroG) / sensibilidad
Ahora tenemos los 3 componentes que definen nuestro vector de fuerza inercial, si el dispositivo no está sujeto a otras fuerzas de gravitación, podemos asumir que esta es la dirección de nuestro vector de la fuerza de gravitación. Si desea calcular la inclinación del dispositivo concerniente a la tierra se puede calcular el ángulo entre este vector y el eje Z. Si usted también está interesado en dirección al eje de inclinación puede dividir este resultado en 2 componentes: inclinación en el eje X y Y que puede calcularse como el ángulo entre el vector de gravitación y X / Y ejes. Cálculo de estos ángulos es más simple que usted puede pensar, ahora que hemos calculado los valores de Rx, Ry y Rz. Volvamos a nuestro último modelo de acelerómetro y hacer algunas anotaciones adicionales:
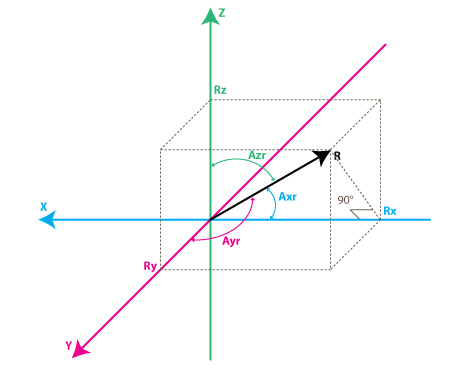
Los ángulos que nos interesa son los ángulos entre X, Y, Z ejes y la fuerza del vector R. Definiremos estos ángulos como Axr, Ayr, Azr. Se nota desde el triángulo de ángulo recto formado por R y Rx que:
cos(AXR) = Rx / R y del mismo modo:
cos(Ayr) = Ry / R
cos(AZR) = Rz / R
Podemos deducir de Eq.1 eso R = SQRT (Rx ^ 2 + Ry ^ 2 + Rz ^ 2).
Podemos encontrar ahora nuestros ángulos mediante el uso de arccos() función (la función cos() inversa):
AXR = arccos(Rx/R)
Ayr = arccos(Ry/R)
AZR = arccos(Rz/R)
Hemos recorrido un largo camino para explicar el modelo de acelerómetro, sólo para llegar a estas fórmulas. Dependiendo de sus aplicaciones puede utilizar cualquier fórmulas intermedios que hemos derivado. También podrá presentar el modelo del giroscopio pronto, y vamos a ver cómo se pueden combinar datos de acelerómetro y giroscopio para proporcionar estimaciones más precisas de inclinación.
Pero antes de hacerlo vamos a hacer algunas anotaciones más útiles:
cosX = cos(Axr) = Rx / R
cosY = cos(Ayr) = Ry / R
cosZ = cos(Azr) = Rz / R
Este triplete se denomina Coseno de la dirección , y básicamente representa el vector de la unidad (vectores con longitud 1) que tiene la misma dirección que el vector R. Se puede verificar fácilmente:
SQRT (cosX ^ 2 + cosY ^ 2 + cosZ ^ 2) = 1
Esta es una propiedad agradable ya que nos absuelven de seguimiento modulus(length) del vector R. Muchas veces si estamos sólo interesados en la dirección de nuestro vector de inercia, tiene sentido para normalizar su módulo para facilitar otros cálculos.













