Paso 3: Combinando el acelerómetro y giróscopo

Juntándolo todo, combinando datos de acelerómetro y giroscopio.
Si estás leyendo este artículo usted probablemente adquirido o está planeando adquirir un dispositivo IMU, o probablemente planea construir uno de independiente acelerómetro y giroscopio dispositivos.
El primer paso en el uso de un dispositivo IMU de combinación que combina un acelerómetro y un giroscopio es alinear sus sistemas de coordenadas. La forma más sencilla de hacerlo es elegir el sistema de coordenadas del acelerómetro como el sistema de coordenadas de referencia. Hojas de datos de acelerómetro mayoría mostrará la dirección de X, Y, Z ejes en relación con la imagen del chip físico o el dispositivo. Por ejemplo, aquí están las direcciones de X, Y, Z ejes como se muestra en las especificaciones de la Junta de Acc_Gyro :

Pasos a seguir son:
- Identificar las salidas de giroscopio que corresponden a RateAxz, RateAyz los valores mencionados. Determinar si estas salidas deben invertirse debido a la posición física del giroscopio en relación con el acelerómetro
No se supone que si un giroscopio tiene una salida marcado con X o Y, corresponderá a cualquiera de los ejes en el sistema de coordenadas de acelerómetro, aunque esta salida es parte de una unidad IMU. La mejor forma es probarlo. Suponiendo que se fija la posición del giroscopio en relación con el acelerómetro. Se supone que las fronteras del giróscopo y acelerómetro son paralelas entre sí, es decir, coloca el giro en un ángulo múltiplo de 90deg en relación con el chip acelerómetro. Si usted adquirió un tablero IMU, lo más probable es que ya están alineados de esta manera. No vamos a discutir en este modelos de artículo donde giroscopio se coloca en un ángulo irregular en relación con acelerómetro (digamos 30 o 45 grados), aunque esto podría ser útil en algunas aplicaciones.
Aquí es una secuencia de la muestra para determinar que la salida del giróscopo corresponde al valor de RateAxz mencionado.
-a partir de colocar el dispositivo en posición horizontal. Salidas X y Y del acelerómetro voltaje de la salida del zero-g (por ejemplo para Acc_Gyro del tablero esto es 1. 65V)
-al empezar a girar el aparato alrededor del eje Y, otra forma de decirlo es que gire el dispositivo en el plano XZ, acelerómetro X y Z salidas de cambio y salida Y se mantiene constante.
-girando el dispositivo en una nota de velocidad constante que giroscopio cambios de salida, las otras salidas de giroscopio deben permanecer constante
-la salida del giróscopo que cambió durante la rotación alrededor del eje Y (rotación en el plano XZ) proporcionará el valor de entrada para AdcGyroXZ, de la cual calculamos RateAxz
-el paso final es garantizar el sentido de giro corresponde a nuestro modelo, en algunos casos quizás tenga que invertir el valor de RateAxz debido a la posición física del giroscopio en relación con el acelerómetro
-realizar nuevamente la prueba anterior, girar el aparato alrededor del eje Y, esta vez monitorizar la salida X del acelerometro (AdcRx en nuestro modelo). Si AdcRx crece (los primeros 90 grados de rotación desde la posición horizontal), entonces AdcGyroXZ también debe crecer. De lo contrario necesita invertir RateAxz, puede lograr esto mediante la introducción de un factor muestra Eq.3, como sigue:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / sensibilidad, donde InvertAxz es 1 o -1
misma caña de prueba hacer para RateAyz, haciendo girar el aparato alrededor del eje X, y se pueden identificar que salida de giroscopio corresponde a RateAyz, y si necesita ser invertida. Una vez que tengas el valor para InvertAyz, debe utilizar la siguiente fórmula para calcular RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / sensibilidad
Si usted haría estas pruebas a bordo de Acc_Gyro se consigue tras los resultados:
-el pin de salida para RateAxz es GX4 y InvertAxz = -1.
-el pin de salida para RateAyz es GY4 y InvertAyz = -1
Partir de este punto lo consideramos que tenga configuración de la IMU de tal manera que puede calcular los valores correctos para Axr, Ayr, Azr (como definida parte 1. Acelerómetro) y RateAxz, RateAyz (como se define en la parte 2. Giroscopio). A continuación analizaremos las relaciones entre estos valores que resultan útiles para obtener la estimación más precisa de la inclinación del dispositivo con respecto al plano de tierra.
¿Usted podría estarse preguntando por este punto, si modelo de acelerómetro ya nos dio los ángulos de inclinación de Axr, Ayr, Azr por eso que queremos molestar con los datos del giroscopio? La respuesta es simple: datos de acelerómetro no siempre se puede confiar 100%. Hay varios motivos, recuerda que el acelerómetro mide la fuerza inercial, dicha fuerza puede ser causada por la gravitación (e idealmente solamente por la gravitación), pero también puede ser causada por la aceleración (movimiento) del dispositivo. Como resultado incluso si el acelerómetro está en un estado relativamente estable, es todavía muy sensible a la vibración y el ruido mecánico en general. Esta es la razón principal por qué la mayoría sistemas IMU utilizan un giroscopio para suavizar cualquier error de acelerómetro. Pero, ¿cómo se hace? ¿Y es que el giroscopio libre de ruido?
El giroscopio no es libre de ruido sin embargo porque mide la rotación es menos sensible a los movimientos mecánicos lineales, del tipo de ruido sufre ese acelerómetro, sin embargo giroscopios tienen otros tipos de problemas como por ejemplo deriva (no va a volver a eco-préstamo valor cuando la rotación se detiene). Sin embargo promediando datos de acelerómetro y giroscopio podemos obtener una estimación relativamente mejor de la actual inclinación del dispositivo que obtendría utilizando los datos del acelerómetro solo.
En los próximos pasos que voy a introducir un algoritmo que se inspiró en algunas ideas utilizados en el filtro de Kalman, sin embargo es mucho más simple y más fácil de implementar en dispositivos embebidos. Antes de eso vamos a ver primero lo que queremos nuestro algoritmo para calcular. Bueno, es la dirección del vector de la fuerza de gravitación R = [Rx, Ry, Rz] de que podemos obtener otros valores como cosZ Axr, Ayr, Azr o cosX, acogedor, que nos dará una idea de la inclinación de nuestro dispositivo con respecto al plano de tierra, discutimos la relación entre estos valores en la parte 1. ¿Uno podría decir: no tenemos estos valores Rx, Ry, Rz de la EC.2 en la parte 1? Bueno sí, pero recuerde que estos valores se derivan de datos de acelerómetro, por lo que si sería utilizar directamente en su aplicación podría obtener más ruido que puede soportar su solicitud. Para evitar más confusión vamos a redefinir las mediciones del acelerómetro como sigue:
RACC - es el vector de fuerza inercial medida por el acelerómetro, que consta de los siguientes componentes (proyecciones en X, Y, Z ejes):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / sensibilidad
RyAcc = (AdcRy * Vref / 1023 - VzeroG) / sensibilidad
RzAcc = (AdcRz * Vref / 1023 - VzeroG) / sensibilidad
Hasta ahora tenemos un conjunto de valores que podemos obtener exclusivamente de los valores de ADC de acelerómetro. Llamaremos a este conjunto de datos de un "vector" y usaremos la siguiente notación.
RACC = [RxAcc, RyAcc, RzAcc]
Porque estos componentes de la Racc pueden obtenerse datos de acelerómetro, podemos considerarlo una entrada a nuestro algoritmo.
Tenga en cuenta que debido a que Racc mide la fuerza de gravitación que será correcto si se asume que la longitud de este vector definida así es igual o cerca de 1 g.
| RACC| = SQRT(RxAcc^2 +RyAcc^2 + RzAcc^2),
Sin embargo para asegurarse que tiene sentido para actualizar este vector como sigue:
RACC(Normalized) = [RxAcc / | RACC| , RyAcc / | RACC| , RzAcc / | RACC|].
Esto asegurará que la longitud de su vector normalizado del Racc es siempre 1.
A continuación te presentamos un nuevo vector y que llamaremos
Resto = [RxEst, RyEst, RzEst]
Se trata de la salida de nuestro algoritmo, estos son valores corregidos en base a datos de giroscopio y basado en datos estimados anteriores.
Aquí es lo que hará nuestro algoritmo:
-acelerómetro nos dice: «Ahora estás en posición de Racc»
-decir "Gracias, pero me deja ver",
-entonces corregir esta información con datos de giroscopio, así como con los últimos datos de descanso y salida de un nuevo vector Estimado resto.
-Consideramos resto que nuestra "mejor apuesta" en cuanto a la posición actual del dispositivo.
Vamos a ver cómo podemos hacer que trabajar.
Comenzaremos nuestra secuencia por confiar en nuestro acelerómetro y asignación:
Rest(0) = Racc(0)
Por cierto recordar resto y Racc son vectores, por lo que la ecuación anterior es sólo una forma simple de escribir 3 sistemas de ecuaciones y evitar la repetición:
RxEst(0) = RxAcc(0)
RyEst(0) = RyAcc(0)
RzEst(0) = RzAcc(0)
A continuación vamos a hacer mediciones regulares a intervalos de tiempo iguales de T segundos, y a obtener nuevas mediciones que definiremos como Racc(1), Racc(2), Racc(3) y así sucesivamente. También podrá emitir nuevas estimaciones en cada intervalos de tiempo Rest(1), Rest(2), Rest(3) y así sucesivamente.
Supongamos que estamos en el paso n. Tenemos dos sistemas conocidos de valores que nos gustaría utilizar:
Rest(n-1) - nuestra estimación anterior, con Rest(0) = Racc(0)
RACC(n) - nuestra actual medición del acelerómetro
Antes de que podemos calcular Rest(n), vamos a introducir un nuevo valor medido, que podemos obtener de nuestro giroscopio y una estimación previa.
Nosotros lo llamamos Rgyro, y también es un vector de 3 componentes:
Rgyro = [RxGyro, RyGyro, RzGyro]
A calcular este componente de un vector a la vez. Empezaremos con RxGyro.
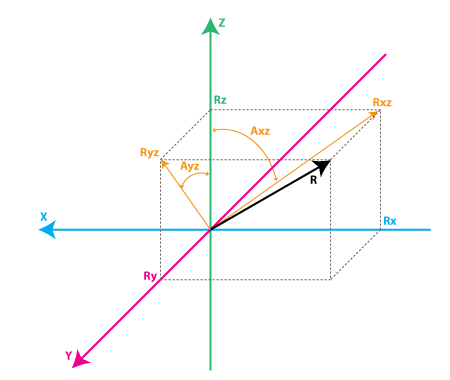
Comencemos por observar a la siguiente relación en nuestro modelo de giroscopio, el triángulo de ángulo recto formado por Rz y Rxz que podemos derivar:
tan(Axz) = Rx/Rz = > Axz = atan2(Rx,Rz)
Atan2 puede ser una función que nunca antes, es similar a atan, excepto devuelve valores en rango de (-PI, PI) como (-PI/2, PI/2) devuelto por atan y se toma 2 argumentos en vez de uno. Nos permite convertir los valores de Rx, Rz a los ángulos en la gama completa de 360 grados (-PI a PI). Puedes leer más sobre atan2 aquí.
Así que sabiendo RxEst(n-1) y RzEst(n-1) podemos encontrar:
Axz(n-1) = atan2 (RxEst(n-1), RzEst(n-1)).
Recuerde que giroscopio mide la tasa de cambio del ángulo Axz. Así podemos calcular el ángulo nuevo Axz(n) como sigue:
Axz(n) = Axz(n-1) + RateAxz(n) * T
Recuerde que RateAxz puede obtenerse en nuestras lecturas de ADC de giroscopio. Una fórmula más exacta puede utilizar un índice de rotación promedio calculado como sigue:
RateAxzAvg = (RateAxz(n) + RateAxz(n-1)) / 2
Axz(n) = Axz(n-1) + RateAxzAvg * T
Del mismo modo que podemos encontrar:
AYZ(n) = Ayz(n-1) + RateAyz(n) * T
OK así que ahora tenemos Axz(n) y Ayz(n). ¿Hacia dónde vamos desde aquí a deducir RxGyro/RyGyro? De la ecuación 1 podemos escribir la longitud del vector Rgyro como sigue:
| Rgyro| = SQRT(RxGyro^2 + RyGyro^2 + RzGyro^2)
También porque hemos normalizado nuestros vectores de Racc, suponemos que su longitud es 1 y no ha cambiado después de la rotación, así que es relativamente seguro escribir:
| Rgyro| = 1
Vamos a adoptar una notación más corta temporal para los cálculos siguientes:
x = RxGyro, y = RyGyro, z = RzGyro
Usando las relaciones anteriormente podemos escribir:
x = x / 1 = x / SQRT(x^2+y^2+z^2)
Vamos a dividir numerador y denominador de la fracción por SQRT (x ^ 2 + z ^ 2)
x = (x / SQRT (x ^ 2 + z ^ 2)) / SQRT ((x ^ 2 + y ^ 2 + z ^ 2) / (x ^ 2 + z ^ 2))
Tenga en cuenta que x / SQRT (x ^ 2 + z ^ 2) = sin(Axz), así:
x = sin(Axz) / SQRT (1 + y ^ 2 / (x ^ 2 + z ^ 2))
Ahora multiplica numerador y denominador de la fracción interior SQRT de z ^ 2
x = sin(Axz) / SQRT (1 + y ^ 2 * z ^ 2 / (z ^ 2 * (x ^ 2 + z ^ 2)))
Observe eso z / SQRT (x ^ 2 + z ^ 2) = cos(Axz) e y / z = tan(Ayz), así que finalmente:
x = sin(Axz) / SQRT (1 + cos (Axz) ^ 2 * tan (Ayz) ^ 2)
Volviendo a nuestra notación obtenemos:
RxGyro = sin(Axz(n)) / SQRT (1 + cos(Axz(n)) ^ 2 * tan(Ayz(n)) ^ 2)
del mismo modo nos encontramos con que
RyGyro = sin(Ayz(n)) / SQRT (1 + cos(Ayz(n)) ^ 2 * tan(Axz(n)) ^ 2)
Ahora, finalmente podemos encontrar:
RzGyro = signo (RzGyro) * SQRT (1 - RxGyro ^ 2 - RyGyro ^ 2).
Donde Sign(RzGyro) = 1 cuando RzGyro > = 0 y Sign(RzGyro) =-1 cuando RzGyro < 0.
Una forma sencilla de estimar esta debe tomar:
Sign(RzGyro) = Sign(RzEst(n-1))
En la práctica tenga cuidado cuando RzEst(n-1) está cerca de 0. Usted puede saltarse la fase de giro en conjunto en este caso y asignar: Rgyro = Rest(n-1). RZ se utiliza como referencia para el cálculo de ángulos Axz y Ayz y cuando está cerca de 0, los valores pueden oveflow y gatillo malos resultados. Vas a estar en dominio de la flotación grande punto números donde cos() / implementaciones de la función atan() pueden carecer de precisión.
Así que recapitulemos lo que tenemos hasta ahora, estamos en el paso n de nuestro algoritmo y hemos calculado los siguientes valores:
RACC - lecturas actuales de nuestro acelerómetro
Rgyro - obtenida de Rest(n-1) y actual giroscopio lecturas
¿Valores que utilizamos para calcular la estimación actualizada Rest(n)? Probablemente adivinaron que vamos a utilizar ambos. Vamos a utilizar un promedio ponderado, por lo que:
Rest(n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Podemos simplificar esta fórmula dividiendo numerador y denominador de la fracción por w1.
Rest(n) = (Racc * w1/w1 + Rgyro * w2/w1) / (w1/w1 + w2/w1)
y después sustituyendo w2/w1 = wGyro que obtenemos:
Rest(n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
En la forumula anterior wGyro nos dice cuánto confiamos en nuestro giro en comparación con el acelerómetro. Este valor puede ser elegido experimentalmente generalmente valores entre 5..20 activarán buenos resultados.
La principal diferencia de este algoritmo de filtro de Kalman es que este peso es relativamente fija, mientras que en Kalman filtro que los pesos se actualizan permanentemente basado en el ruido medido de las lecturas del acelerómetro. Filtro de Kalman se centra en que le da resultados teóricos "lo mejor", considerando que este algoritmo puede dar resultados "suficientemente bueno" para su aplicación práctica. Puede implementar un algoritmo que se ajusta wGyro dependiendo de algunos factores de ruido que se mide, sino valores fijos funciona bien para la mayoría de las aplicaciones.
Estamos a un paso de conseguir nuestros valores estimados actualizados:
RxEst(n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro)
RyEst(n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro)
RzEst(n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Ahora vamos a normalizar este vector otra vez:
R = SQRT(RxEst(n) ^ 2 + RyEst (n) ^ 2 + RzEst (n) ^ 2)
RxEst(n) = RxEst (n) / r
RyEst(n) = RyEst (n) / r
RzEst(n) = RzEst (n) / r
Y ya estamos listos para repetir el bucle.
Esta guía apareció originalmente en starlino.com, he hecho algunas ediciones luz y volver a la publicada con permiso. Gracias Starlino!













