Paso 5: Resolver las fuerzas reaccionarias de braguero
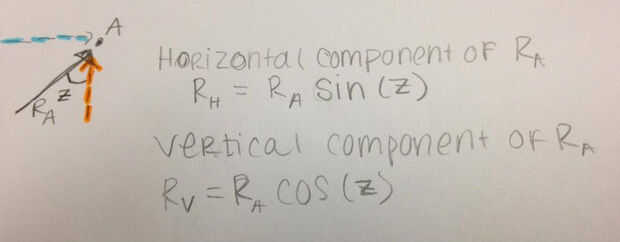

Usando el diagrama de cuerpo libre que ha solo dibujado de la armadura entera que podrás resolver por las fuerzas reaccionarias.
Para ello escribes tres ecuaciones. Estas ecuaciones provienen del hecho de que el truss es estacionaria o inmóvil. Para la armadura permanezca estacionario, las fuerzas que experimenta en la dirección horizontal deben cancelar uno al otro, y las fuerzas en la dirección vertical también deben cancelar.
La primera ecuación está escrita para las fuerzas en la dirección vertical. Se denotan las fuerzas hacia abajo que hacia arriba y negativas las fuerzas positivas. Las fuerzas verticales son todos suman e iguales a cero.
La segunda ecuación se escribirá para las fuerzas en la armadura en la dirección horizontal. Se indican fuerzas hacia la derecha positivo y hacia la izquierda negativo. Asimismo, las fuerzas horizontales se ha añadido y fijar iguales a cero.
La tercera ecuación es la suma de los momentos de las fuerzas que actúan sobre la armadura. Un momento es una medida de la tendencia de una fuerza para hacer que el objeto gire alrededor de un punto fijo. Un momento es igual a la fuerza multiplicada por la distancia perpendicular desde el punto fijo.
Hemos elegido para nuestro punto fijo, A. El punto en el cual se suman los momentos es arbitrario, pero la mejor opción es un punto que tiene varias fuerzas actuando directamente sobre ella. Fuerzas que actúan directamente sobre el punto no considerado en la ecuación de momento. Elegimos un punto porque los componentes vertical y horizontales de Ra por lo tanto no se consideran en la ecuación. La suma de los momentos sobre el punto fijo son suman e igual a cero.
** Si la fuerza que actúa sobre el cuerpo hará que el cuerpo gire hacia la izquierda, como Rb en este caso, se considera positivo. Si la fuerza hace que el cuerpo gire hacia la derecha, se considera negativo.
Utilizando estas tres ecuaciones y sustitución que podemos resolver para las fuerzas reaccionarias de la armadura.