Paso 2: curva 3D
Ahora tenemos que tomar la red nudo y convertirlo en curvas 3D. Comencemos por asignar un espacio de coordenadas local para nuestra red de nudo.
Así que ahora tenemos (u, v) coordenadas para cada punto de nuestra red. Tenga en cuenta que el nudo se envuelve, por lo que una u de 0 será igual a una u de 1.
Ahora, definamos un cilindro con diámetro D y altura H:
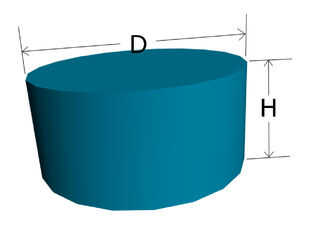
Si fijamos el eje z al eje principal del cilindro y poner el origen en el centro del cilindro, podemos asignar nuestro (u, v) coordenadas de un punto 3D con las siguientes ecuaciones:
x = D/2*cos(360*u)
y = D/2*sin(360*u)
z = -H/2 *(1-v) + H/2 * v
Ahora a pie a través de nuestra red, como se hizo en el primer paso y soltar un punto 3D en cada punto de rejilla usando las ecuaciones anteriores. Entonces podemos conectar los puntos de una curva mediante la interpolación de Catmull-Rom. Tenga en cuenta que en la imagen de abajo H fue fijado a un valor menor que la altura real del cilindro, razón por la cual la curva no va hasta la parte superior e inferior.

Ahora tenemos que compensar los puntos para tener en cuenta cuando damos grosor a la curva, así como overs y unders. Tenemos que compensar los puntos hacia afuera del cilindro en cada punto de rejilla. Para calcular la dirección que necesitamos compensar utilizamos ecuaciones muy similares al anterior, excepto z siempre será 0 y D irrelevent como queremos un vector de longitud unidad:
NX = cos(360*u);
NY = sin(360*u);
NZ = 0;
Después de compensar la curva obtenemos lo siguiente:














