Paso 5: La curva de Koch y copo de nieve
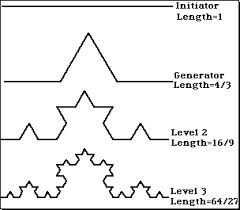

Para crear el Copo de nieve de Koch, Niels Fabian Helge von Koch comenzó con la Curva de Koch ya había desarrollado. La Curva de Koch comienza con una línea recta que se divide en tres partes iguales. El segmento medio se utiliza como base, y se forma un triángulo equilátero. Luego, se retira la base del triángulo, mostrando la primera iteración de la curva de Koch.
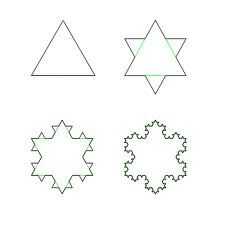
El copo de nieve de Koch es un derivado de la Curva de Koch. El copo de nieve comienza con un triángulo equilátero. Los pasos en la creación de la curva de Koch se aplican repetidamente a cada lado del triángulo equilátero, creando una forma de "copo de nieve" a la forma.
Al igual que varios otros fractales, Copo de nieve de Koch es self-similar, proyectando la misma imagen en cualquier escala.
El número de iteraciones es la cantidad de pasos de la forma original de origen de los fractales. Sin embargo, la forma original se cuenta generalmente como la primera iteración. Holísticamente, encontramos que mientras que un mayor número de iteraciones induce mejor recepción de canales en el Fractal de la soldadura y los fractales de papel de aluminio, un diseño simple de 2 iteración Fractal de alambre aislado produce el mismo número de canales como el de la antenas de Fractal de la soldadura.













