Paso 4: Puertas lógica
Ahora echemos un vistazo a cómo se utilizan MOSFETs en cálculos de lógica.
Bueno, quisiera volver a un paso. Para entender de informática, debe tener un conocimiento básico del álgebrade Boole. Si no está familiarizado con el álgebra boleana, parar aquí y hacer algunas investigaciones. Probaré y simplificarlo, pero electrónica-tutorials.ws tiene un gran conjunto de enseñanzas específicamente orientadas a la electrónica o digital, lógica. La BBC tiene un fresco sitio interactivo para el aprendizaje de lógica digital también. Lógica digital es lo que usamos para el diseño de procesadores de computadora lógica. También puede aprender más sobre mapas de K, que le permiten ver complejas tablas de verdad de una manera diferente (y a menudo más fácil) y teoremas de Morgan, que son la base del álgebra de Boole. En un sentido más amplio, material de referencia en matemáticas discretas, que abarca la lógica pero también teoría de conjuntos, recursividad y relaciones, también puede venir práctico. Wikipedia tiene una lista de operadores que se utilizan para las expresiones de la lógica. También, a modo de aclaración, en lógica digital utilizamos 1 (encendido) y 0 (apagado) para indicar el estado de la entrada o salida.
Ahora echemos un vistazo a cómo se utilizan MOSFETs en cálculos de lógica, vamos.
Primero una teoría
La primera puerta de la lógica que quiero introducir es la puerta de entrada dos y porque probablemente es la lógica más fácil de entender. La imagen de abajo muestra el símbolo esquemático para una puerta y.
La salida de la puerta y sólo será alta si las entradas son también altas. Si cualquier entrada es baja, la salida también es baja. El símbolo (en lógica digital) es "●". Consulte la siguiente tabla para la tabla de verdad puerta AND.
| A | B | A • B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Al mirar las tablas de verdad, el número de resultados posibles en la columna derecha se relaciona con el número de entradas elevando 2 a una potencia igual al número de entradas. En otras palabras, si tiene dos entradas, tiene 22 = 4 salidas. Con 3 entradas, usted obtiene 23 = 8 salidas y con 8 entradas su get 28 = 256 salidas posibles.
La segunda puerta a considerar es la puerta NAND, no y no es la manera que describimos negación o decir algo es lo contrario. La negación de true es false y no del y NAND. El símbolo de no (en lógica digital) es la tilde "~". La tabla de verdad NAND es similar, pero opuesto a la tabla de verdad y. Consulte a continuación.
| A | B | ~(A • B) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La columna de salida es todo lo contrario de la salida y de tabla de verdad, ¿no? Otras tablas de verdad (y puertas así) son o, o, XOR, XNOR y no. Te remito a esta página para una lista completa de las tablas de verdad en lógica digital y los símbolos de esquema asociados.
Ahora algunas aplicaciones
¿¿Vienen MOSFETs jugar con puertas lógicas? Bueno, ya que MOSFETs son tan fáciles de saturar (vuelta completamente encendido) con bajo voltaje y la corriente casi insignificante, podemos construir las puertas de la lógica anteriormente con ellos y a su vez construir sistemas de lógica digital extremadamente confiable para procesar datos. Vamos a ver cómo una puerta no se ve en el interior y ver si podemos hacer algún sentido de este. Estoy empezando con el no porque tiene el menor número de MOSFETs para construir y por lo tanto debe ser menos confuso. Ver el esquema abajo.
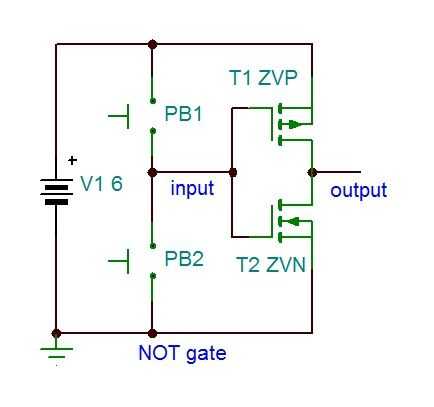
La puerta no se utiliza, como su nombre lo indica, para negar o para invertir la señal de entrada. PB1 conecta las dos puertas MOSFET a + 6V, pero sólo la ZVN abrirá con voltaje positivo. Cuando se abre cuando se conecta la salida a la tierra, así que el + entrada se convierte en tierra en la salida. Por el contrario, cuando aplicamos GND a la entrada a través de PB2, sólo la ZVP se abre, que conecta la salida de + 6V, otra vez invirtiendo la señal. (Cuando se presiona ningún botón, la salida puede 'flotar' y o + V o GND, así que es común para forzar la entrada a un estado para garantizar que usted sabe lo que la salida es en ese momento. Una manera simple de hacer esto es reemplazar a cualquiera de los botones con un resistor de 1kΩ, forzando la entrada a ese potencial cuando no se presiona el botón restante. Puedes elegir cuál es su estado de inactividad así.) Os animo a construir esto, pero no detallo las instrucciones.
Ahora vamos a ver lo que una puerta del NAND parece dentro. Esta vez estamos utilizando 4 MOSFETs. Ver el esquema abajo.
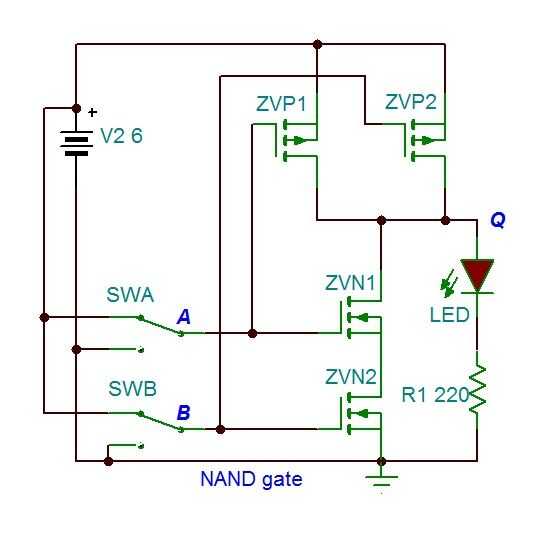
El LED apagará sólo (lógica 0) cuando los SWA y SWB son altos (lógica 1). ¿(Nota cómo el LED del símbolo en el esquema es casi negro, que indica? Recuerde). Compare este resultado con la tabla de verdad NAND. Otra vez me animo a construir esto, pero no se como pasos de compilación.
¿Lo que obtenemos cuando mezclamos los dos? ¿Si la NAND es un no y y se combinan con un segundo no, lo que obtenemos? ¿No es eso sólo una negativa doble? Tan las NOTs cancelar, lógicamente, y estamos a la izquierda con una puerta y. En álgebra boleana, la ecuación parece ~ (~(A●B))⇔(A●B). Bastante limpio. A continuación está la tabla de verdad para en caso de hace más fácil de entender. También a continuación es el esquema, al que he añadido algunas etiquetas para clarificación.
| A | B | (A • B) | ~(A • B) | ~(~(A • B)) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
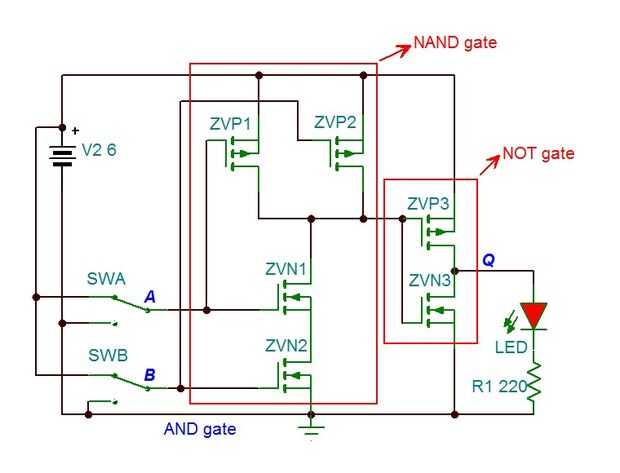
Si comparas los esquemas para el y no puertas NAND, verás que a pesar de que en el exterior la NAND es la negación de y, en el interior la puerta y realmente está hecha de una puerta NAND seguida por una puerta no. Así que como dije arriba, la puerta y es realmente una NAND no. No te preocupes, me tomó un tiempo para coger aquél también. Tenga en cuenta también cómo el LED en el esquema es rojo brillante, indicando que es de cuando los interruptores están en. Compara eso con la NAND gate esquemática imagen de arriba.
A continuación se muestran esquemas para la OR y XOR. Notar que ambos son en realidad una combinación de sus respectivas inversas (NOR y XNOR) con una puerta que no.
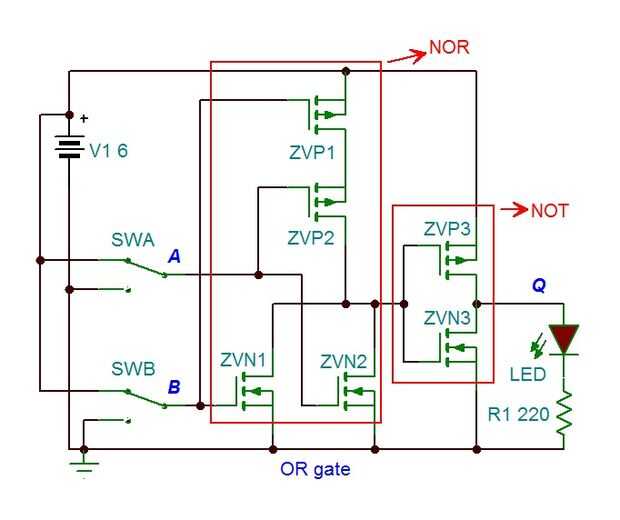
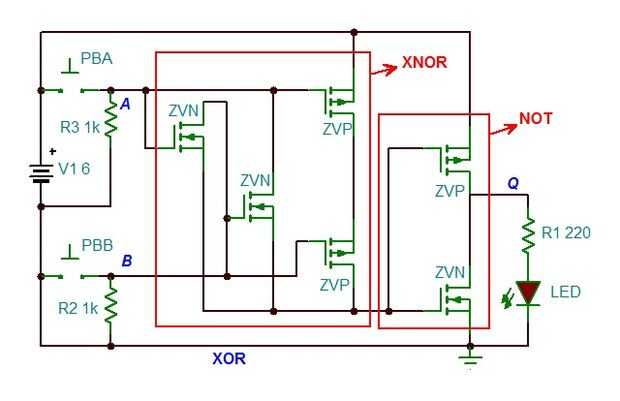
En verdad puede ser probado que cualquier puerta lógica y por lo tanto cualquier circuito lógico, se pueden construir con un número finito de puertas NAND. Además, chips FPGA y los tableros diseñados alrededor de ellos le permiten escribir código (usando VHDL o Verilog) que conectará las puertas como sea necesario para completar el circuito y es una manera muy fácil para empezar a construir e implementar circuitos lógicos digitales. ¿Teniendo en cuenta lo difícil que puede ser alambre encima de una puerta lógica, te imaginas tratando de conectar un circuito de lógica todo usando MOSFET discreto? Sólo ha sido posible en los últimos años para los estudiantes y aficionados poder construir circuitos como serpientes, que son simples en teoría pero compleja de construir, debido al avance de la tecnología y la miniaturización de las partes implicadas. En fin, estoy divagando. Estoy tan agradecido por la tecnología que está a nuestro alcance, cuando no hace mucho tiempo era sólo un deseo.
Así que ahora que está tan clara como el barro, continuemos. Ahora que ya tenemos puertas, ¿qué podemos hacer con ellos?













