Paso 5: circuitos de lógica
Los circuitos aquí serán muy simples, pero requerirán un gran número de N-ch y ch P MOSFET o lógica ICs. Lógica ICs son baratos y fáciles de encontrar (prueba este enlace para el IC 4001) o este enlace para el IC 7402, que son ambos cuatro puertas NOR, por lo que no será demasiado difícil.
Los circuitos de vinieron del libro de Forrest Mims proyectos de lógica Digital: Libro II. Aquí hay un enlace al PDF de RadioShack, o a Amazon.com para su compra. (Como nota, recomiendo conseguir electrónica básica: transistores y circuitos integrados: libro así, también de Forrest Mims. Amazon.com o PDF)
Algunas cosas para recordar cuando se trabaja con la lógica ICs:
- Asegúrese de evitar la acumulación estática de descarga para evitar dañar los chips.
- Cada chip tiene un pin común de + V y un pin GND común. Estos no aparecen en los esquemas, pero deben ser fáciles de encontrar en la hoja de datos (datasheet 7402).
- Las patas de entrada que no se utilizan deben ser conectadas a tierra. Esto también no aparecerá en los esquemas.
- Chips de lógica no deben ser drivers de corriente alta para cargas grandes como motores y tal. Sin embargo pueden ser utilizados para cargas pequeñas, como un LED, o para proporcionar la señal para estos conductores, como en el paso 3
Para los esquemas siguientes, tenga en cuenta el número de SN74XX por encima de cada puerta. Es el número de IC que usa para construir los circuitos si usted quiere conseguir algunos ICs y construir en su propio. La mayoría de estos chips viene con 4 de la puerta específica, así que el SN7402 a continuación tendría 4 puertas NOR.
OK, empecemos con un simple LED flasher. Con sólo dos puertas NOR, podemos construir un oscilador. Ver esquema de más abajo.
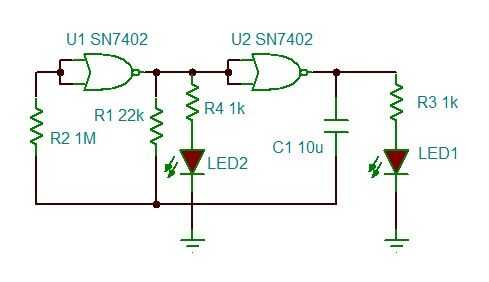
LED2 y R4 son opcionales si usted quiere tener dos LEDs que flash hacia adelante y hacia atrás. De lo contrario LED1 se flash encendido/apagado a una tasa determinada por los valores de R1 (intentar aquí un potenciómetro) y C1.
El siguiente circuito es un cierre de set/reset, que es un componente clave de lógica secuencial. Cierres forman la base de la memoria de la computadora, ya que la salida permanece encendido incluso después de soltar el interruptor. Un grupo de 8 cerraduras formarían la estructura del núcleo de una célula de memoria de 8 bits. En la memoria, el latch SR es conocido como un latch D (datos) y se usa con el reloj del núcleo del sistema para determinar cuándo cierre. (Hay más a él, pero está fuera del alcance de este I'ble. Mira aquí para más información sobre cómo funciona la memoria de la computadora y aquí para una comparación entre la lógica combinacional y secuencial.) Ahora, el esquema.
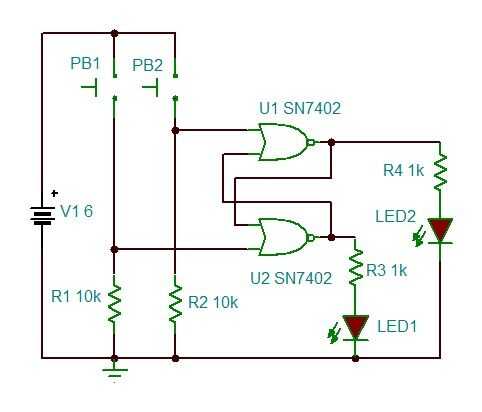
Este circuito es más una demostración de concepto ya que nos interesa generalmente solamente una salida del pestillo porque como el flip-flop de salidas entre Estados como se pulsan los botones, siempre estarán en Estados opuestos uno al otro. Puede atar a una de las salidas aquí para un segundo circuito y utilizar el pestillo como un interruptor no mecánicos "empujar / empujar", del segundo circuito.
Como se mencionó anteriormente, cualquier compuerta lógica o circuito puede hacerse de un número finito de puertas NAND. Aquí es un ejemplo de una puerta OR con 3 puertas NAND.
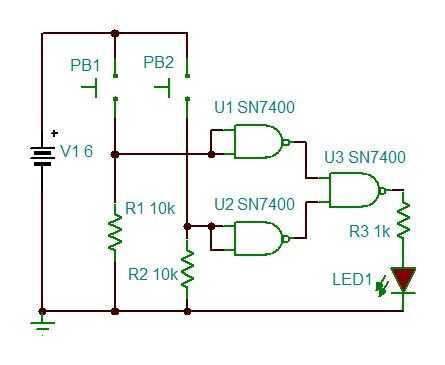
Para cambiar el OR a un NOR, agregar un cuarto NAND entre la salida de U3 y el LED, con las dos entradas de U4 atados juntos.
Parece que sería más costoso utilizar MOSFETs mucho más para hacer la misma cosa (4 para 1 puerta NOR, 16 para 3 puertas NAND) y cuando está diseñando un nuevo chip, el espacio y el número de partes en que el espacio es lo más importante en relación con el costo del chip. Bueno, aquí está el beneficio. ¿Recuerde que los chips FPGA que mencioné antes? Estos son chips genéricos que pueden ser programados para cualquier situación. Si tenemos un cubo enorme de puertas NAND que se puede hacer nada, entonces podemos hacer... nada. Pero si tratamos de ahorrar espacio y costes utilizando puertas específicas, estamos limitados por el número de cada puerta que tenemos. ¿Qué pasa cuando necesitamos más puertas OR? Un rediseño me parece, y cuesta demasiado. El punto es que si ya tienes un diseño específico en mente, puede ser mejor utilizar la puerta exacta que necesitan y no un cajón de puertas NAND genéricos. Pero si eres de prototipado y diseño desde cero, usted necesita flexibilidad, y es donde brillan puertas NAND.
De todos modos, de nuevo a él. Otra vez usando sólo puertas NAND, podemos construir una puerta de XNOR.
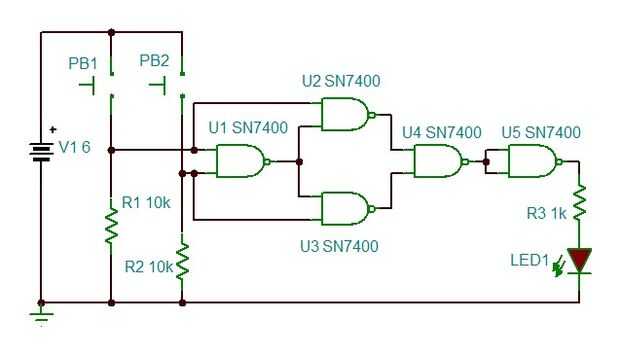
U5 y atar la salida de U4 a R3, tenemos una puerta XOR.
Una sola puerta XOR se puede utilizar como un sumador binario de 1 bit. Mediante la adición de dos puertas NAND (que es sólo una puerta y si te acuerdas), obtenemos un medio sumador con una salida de dos bits.
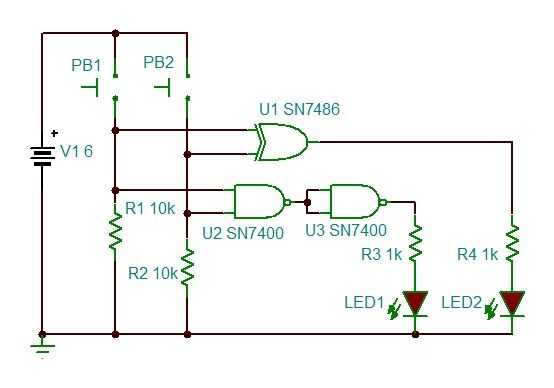
Un full-adder requiere un par de cambios (añadir un XOR, dos NANDs y una puerta OR), que añade una entrada para llevar las señales de un sumador anterior. Varias serpientes entonces se apilan juntos, una serpiente para cada bit, para construir una máquina sumadora. Es realmente muy elegante. Abajo se encuentra un circuito sumador completo.
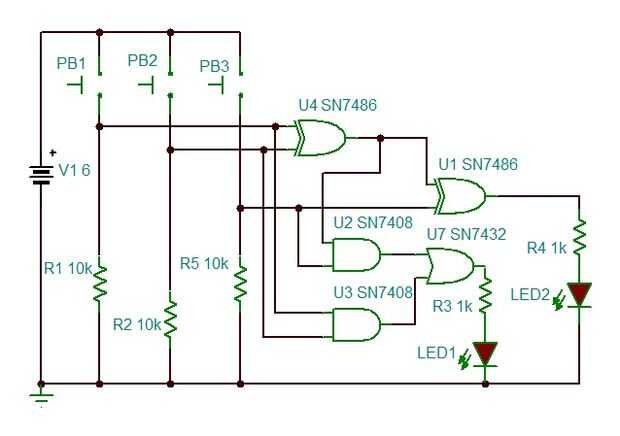
PB1 es un bit, PB2 es de tipo bit B y PB3 es el bit de carry del bloque sumador anterior. Si solo apretamos PB1 o PB2, añadimos 1 + 0 y solamente 2 LED se iluminará para indicar un valor de 1. Si nos junte PB1 y PB2, indica una adición binaria de 1 + 1, que es 10 en binario (indicado como 10b). Que enciende el LED1 y LED2 de dejar fuera. Si luego presione PB3 y añadir 1 más, conseguimos 11b y ambos se iluminan.
Por debajo está un diagrama de bloques de un sumador de 4 bits utilizando 4 cuadras full-adder. El primer bloque de la derecha (con A0 y B0) puede ser intercambiado con un medio sumador con ningún efecto en la salida. Simplemente quita el la lleva en (Cin) en el primer full-adder, que está conectado a GND aquí de todos modos.
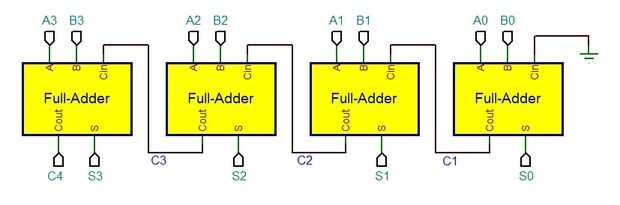
En este ejemplo estamos agregando dos números de 4 bits A y B. Los primeros bits de cada (A0 y B0) se añaden a la derecha, con el resultado enviado a S0 y cualquier bit de carry (C1) enviada a la serpiente siguiente. A1 y B1 se añaden, junto con el C1 de la víbora primera, el resultado va a la salida S1 y cualquier bit de acarreo es enviado a (C2). El último bloque de contactos muestra el bit de carry-out final (C4), o ignora si no hay espacio o si es lo de menos. Que el diseñador llega a tomar esa decisión.
Veamos un ejemplo más de la lógica, una cerradura digital comparador de 4 bits. Como se mencionó, puertas XOR se pueden utilizar como serpientes, pero también son comparadores, presentación de un estado, si ambas entradas son iguales y el estado invertido si ambas entradas son diferentes. Esto nos permite comprobar el estado de un pin y cambiar y sólo de salida si es correcto.
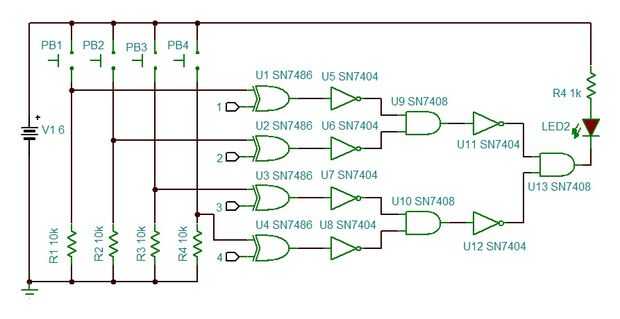
Los pines marcados 1, 2, 3, y 4 son para la programación de la cerradura. Establece estos pines altos o bajos para determinar al combo, y luego tienes que pulsar los botones correspondientes mismo PB1-PB4 en orden para la salida de U13 para ir bajo. Esto permite actual a fluir a través del LED y se enciende. Para establecer el combo usted puede atar bien las patillas directamente a GND o + V o usar algún tipo de dispositivo de memoria que almacenará la entrada una vez y no cambiar. ¿Suena familiar? Sí, usted puede agregar fácilmente un circuito de cierre a los pines set 4 combo. Como los seguros de no perder poder, no perderán el valor almacenado en ellos. Las aplicaciones para esto son simples en el mejor, pero se pone la idea a través de. (Estoy de ninguna manera responsable de cómo usted decide utilizar este circuito ya que no es muy seguro y puede ser fácilmente hackeado/reset).













