Paso 5: Optimización de Balance
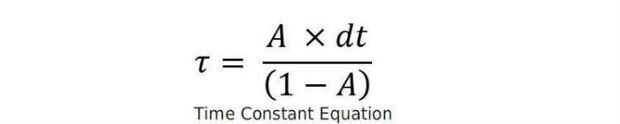
Y ahora llegamos a la parte interesante – cómo mejorar el robot de rendimiento. Tuve algunas ideas sobre dónde empezar a buscar, pero como con cualquier sistema, es difícil saber lo que cruzan las variables son las dependencias. Así que en lugar de obtener demasiado analítico, sólo salté en.
Intervalo de tiempo de lazo de control
Empecé variando el intervalo de tiempo en el que se evaluó el equilibrio PID. Había medido el período de PWM de Arduino 101 por defecto en 2mS, y mi proyecto anterior había utilizado un valor de 20mS así que comenzó a 5mS y duplica el intervalo hasta que el robot no pudo equilibrar. En 5 ms, el robot fue capaz de equilibrar, pero parece ser demasiado activos y oscilado con un período de aproximadamente 120mS. En 10mS, otra vez fue capaz de equilibrar, pero las oscilaciones ralentizado a 280mS. A 20mS, período oscilante recogido hasta 180mS aproximadamente, pero en lugar de activo, la respuesta parecía lenta. En 40mS la respuesta llegó a ser incluso más lento, el balanceo errático y el robot no era siempre capaz de mantener el equilibrio. Mi conclusión fue mientras que el intervalo de evaluación PID sin duda puede influir en el comportamiento del robot, y de hecho tenía que ser por encima de algunos tasa mínima para poder equilibrar, no fue la bala mágica. Para el resto de mis pruebas he utilizado un intervalo de bucle de control de 5mS.
Filtro de la fusión del sensor
Luego me trasladé al filtro de la fusión del sensor. ¿Por qué necesitamos un filtro de la fusión de todos modos? Para responder a esa pregunta, tenemos que examinar el corazón de un sistema de equilibrio, el IMU (unidad de medición inercial). Una IMU consiste en dos tipos de sensores, un giroscopio y un acelerómetro. El giróscopo mide la velocidad angular de cambio o velocidad angular. Teóricamente una buena estimación de posición angular puede generarse mediante la integración de la salida del giróscopo. Por desgracia, sensores de giroscopio tienen un efecto llamado deriva, lo que registrará algunos velocidad angular pequeña incluso al estar muerto todavía. Así que si usted genera su ángulo Estimado sólo mediante la integración de la salida del giróscopo, tienes un error que seguirá aumentando con el tiempo – un problema que hace que una única solución de giroscopio insostenible para el equilibrio. Entrar en el acelerómetro. El valor reportado por el acelerómetro incluirá el efecto de la gravedad, que es constante, así como cualquier otra aceleración, que variará basado en el movimiento del dispositivo. El IMU, es el vector de gravedad que nos interesa. La idea de un filtro de fusión es generar un ángulo estimado mediante la combinación de estos dos sensores. Favorece el giroscopio instantáneamente la salida (pasado a través de un filtro de paso alto) pero la salida del acelerómetro en el largo plazo mediante la medición de dirección gravitacional de la tierra (pasado a través de un filtro de paso bajo) para quitar cualquier deriva.
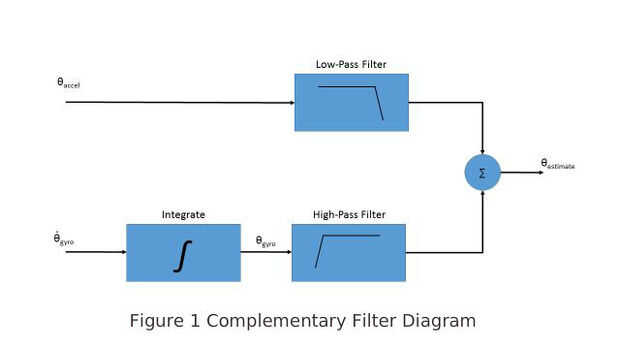
¿OK, así que tenemos un filtro de la fusión, pero que uno? Existen soluciones muy completas y complejas. El filtro de Kalman es uno de los filtros de fusión más prominentes, pero incluso un ingeniero plenamente no puede equipar a entender lo que está en la caja negra. Para este proyecto utilicé una solución similar, pero menos computacionalmente exigente, el filtro Madgwick. Utilicé este filtro por una razón principal: viene incluido con el Arduino 101! Pero la configuración de la IMU en el caso de equilibrio – sólo un grado de libertad, crea limitaciones que nos permiten utilizar una solución más sencilla, el filtro complementario. El filtro complementario recibe su nombre debido a los factores de multiplicación para cada término añadir hasta 1. Un diagrama de bloques de un filtro complementario se muestra en la figura 1.
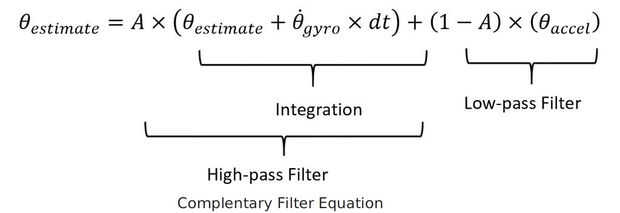
Hay algunos tratamientos muy buenos en la web para los detalles detrás del filtro complementario, sobre que acabo proporciona la ecuación resultante del filtro. En la ecuación, A es una constante que determina las características del filtro. Además, cabe señalar que en los cálculos de ángulo de acelerómetro, estamos tomando ventaja de la aproximación pequeña del ángulo, una realización que para ángulos de menos de ~ 30̊, sin(θ) ≈ θ en radianes. Para nuestro robot, si el ángulo acerca a 30̊, va a caer, por lo que Asunción parece válida. Como resultado podemos saltar la sin(θ) en este cálculo con poco impacto. Por último, la constante de tiempo del filtro complementario también se muestra arriba.
He probado el Madgwick y filtro complementario para ver cómo es afectado el equilibrio del robot. La acción Madgwick filtro instalado la Beta había fijado en 0,1, utilizando una instrucción #define en el archivo de encabezado MadgwickAHRS.h. El robot no se equilibraría con esa configuración, la respuesta fue un poco demasiado lenta. Después de jugar, encontré que habilita un valor de 0.01 el mejor equilibrado, aunque había cierto compromiso en exactitud del ángulo absoluto con esa configuración. Si llevó a cabo el robot en un ángulo por un momento, dicen 20̊ y volvió a vertical, hubo un retraso en el ángulo Estimado regresar a 0̊.
Para el filtro complementario, utilicé A 0,98, que da una constante de tiempo de alrededor de 0,25 segundos, con despegue en 5 milisegundos. Encontré que los resultados sean comparables con el filtro Madgwick y mejor que mi primer proyecto, pero todavía no rock sólido equilibrio. Así continuó la búsqueda.
El uso de retroalimentación de posición (encoders)
Los DC motorreductores seleccioné para este robot incluyen codificadores para proporcionar información sobre el movimiento de la armadura del motor. Los codificadores son del motor antes de que ocurra el engranaje, por lo que proporcionan una muy alta resolución en movimiento - con la relación de engranajes y ruedas de diámetro utilizadas, determina que cada transición de codificador traducida al ~0.04cm. Distancia y velocidad fue bastante sencillos derivar, contando las transiciones del codificador en un intervalo de tiempo regular y luego multiplicando el resultado por 0.04 para obtener distancia y dividiendo esa distancia por el intervalo de tiempo (20mS en mi caso) para obtener velocidad.
Estoy planeando mi próximo proyecto para abordar más plenamente las capacidades de navegación del robot, así que no entraré en mucho detalle aquí, pero se utilizaron dos métodos para controlar la velocidad del robot – ajuste de ángulo objetivo y además directo a los valores PWM motor. Añadir control de velocidad ha quitado por el robot "deambular" pero no mejoró significativamente el equilibrio. En el bucle de control.
Lazo de control de variables y la estructura
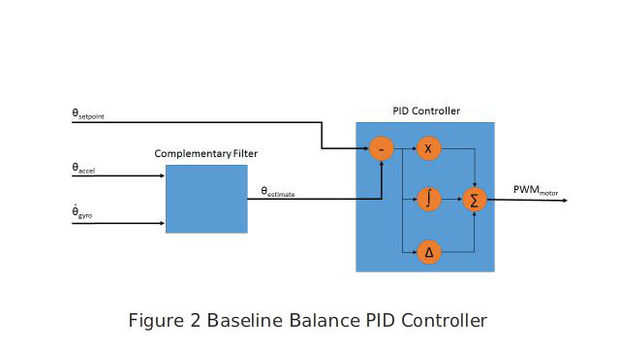
El lazo de control principal para el equilibrio del robot se basa en dos elementos – el filtro de fusión para determinar el ángulo alrededor del robot y un controlador PID con el ángulo estimado para generar la señal de control del motor. La idea detrás de un controlador PID es calcular el error de una señal de control contra un punto de ajuste y luego suma las formas proporcionales, integrales y derivadas de ese error después de que cada uno se han multiplicado por diferentes constantes. El controlador PID muy versátil como elemento de control, con acceso a donde el error ha sido (I), donde está ahora (P) y hacia dónde se dirige (D). Pero estar prevenidos - puede ser una tarea muy difícil para optimizar los multiplicadores de la P, I y D términos. Figura 2 es un diagrama de bloque demostrando la conectividad básica de la estructura y el control y refleja la configuración inicial de este robot.
Sobre una inspección más cercana, usted puede notar que el término de D del controlador PID es tomando el derivado del ángulo estimado, que se traduce en una velocidad angular estimada de cambio. Si recordáis, el giroscopio estaba proporcionando sólo que, una velocidad angular de cambio, sino que es mucho más preciso. Esto nos lleva a preguntarnos cómo se comportaría el bucle de control si la salida del giroscopio se utiliza directamente, en lugar de volver a calcular la velocidad angular del ángulo estimado.
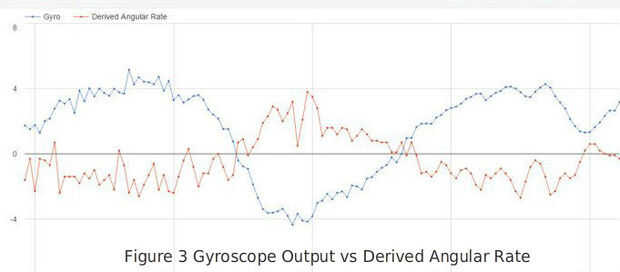
Después de alimentar el giroscopio en el término de D del PID, el cambio en el equilibrio de rendimiento fue notable. Figura 3 da un vistazo a por qué – muestra la salida de giroscopio junto con el término de D de la EPI. La velocidad angular de cambio derivada el ángulo Estimado va a la salida del giróscopo por sobre 150mS, una demora que ayuda a explicar algunos de bamboleo en el equilibrio de la configuración original y le pregunto cómo equilibrado en todo.
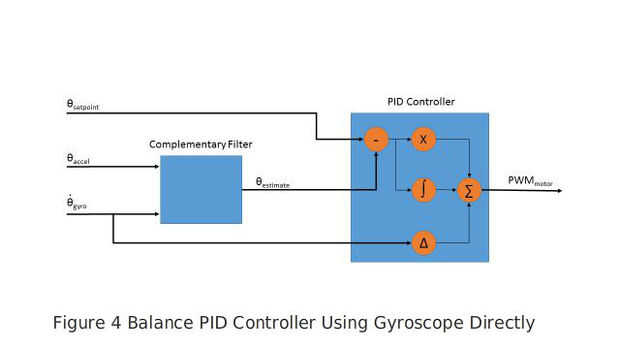
La figura 4 muestra la configuración final, con el giroscopio se alimentan directamente en el término D del controlador PID. Mientras que todas las áreas exploradas tuvieron alguna repercusión sobre el equilibrio de rendimiento, proporciona una indicación de puntuales y mayor fidelidad de la velocidad angular de giroscopio siempre que el cambio en el rendimiento del robot que buscaba.













