Paso 6: Filtro de Kalman
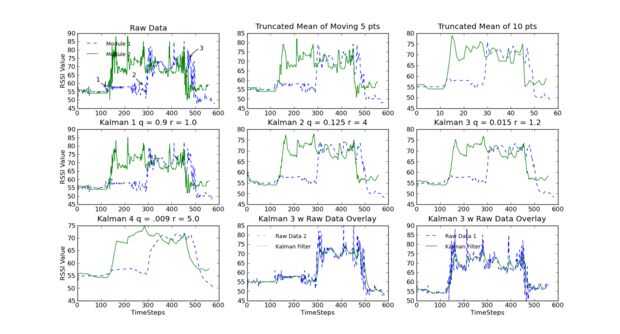
También probar y explicar el filtro aquí.
Resolver de forma recursiva:
p = p + q;
k = p / (p + r); (ganancia)
x = x + k * (rssi_data-x);
p = (1 – k) * p;
Eso es todo!
Condiciones iniciales:
x = x_o (mejor conjetura)
p = p_o (error estimado)
r = r_o (ruido del sensor)
q = valor de q_o (ruido de proceso) entre 0 y 1
Parámetros en negrita quedan estáticos a través de la simulación
¿Cómo elegimos nuestros parámetros? Elección del parámetro es difícil y requiere a menudo mucho masaje. Para obtener una idea de cómo nosotros debemos elegir q y r, echemos un vistazo a ciertos comportamientos extremos:
- Si q es mucho mayor que r, entonces k = 1 y x es simplemente el valor medido.
- Si r es muy pequeño (muy, muy cerca de 0), entonces k = 1 y x es simplemente el valor medido
Esto significa que q/r o r q no debe ser demasiado grande o demasiado pequeño y r debe ser demasiado pequeño. Otra vez, deberás de masaje el parámetro para obtener los datos que desee. He seleccionado 3 Kalman porque es un buen equilibrio entre el tiempo de posposición y filtrado de ruido, donde como Kalman 4 filtra el ruido de muy bien, pero queda demasiado detrás de los datos.
En realidad, matemáticas/programación se puede hacer aún más sencilla si usted asume que el ruido de proceso (q) y el ruido del sensor (r) no cambian con el tiempo. Si están convencidos de que tiene los parámetros correctos, la ganancia de Kalman (k) se estabilizarán eventualmente a un único valor. Puede calcular previamente qué es ese valor y simplificar el filtro:
x = x + k * (rssi_data-x);
Para aquellos interesado también en filtros de Kalman se usa para datos RSSI por favor lea: http://www.cs.tut.fi/sgn/arg/heln/Publications/CSCC2001_Helen.pdf