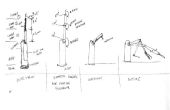
Paso 9: Dos dimensiones cinemática delantera

Para hacer el robot de pintura sobre el lienzo, tendremos que averiguar cómo hacer que se mueva de una manera aceptable, que es, extienda el brazo de tal manera que la punta del pincel no es ni demasiado lejos, ni tratando de llegar a través de la lona. Movemos el brazo mediante el envío de pulsos (que corresponden a los ángulos) a los motores, pero ¿qué ángulos elegimos y cómo sabemos donde están el brazo y el cepillo? Estas preguntas nos llevan al fascinante mundo de la cinemática. Según el la entidad omnisciente web Wikipedia:
Cinemática es la rama de la mecánica clásica que describe el movimiento de puntos, los cuerpos (objetos) y sistemas de órganos (grupos de objetos) sin la consideración de las causas del movimiento.
Ahora, hay dos clases de cinemática: inversa y directa. Cinemática inversa es el más útil de la dos nos permite tener un punto dado, y entonces determinar el movimiento de un cuerpo (sólo el brazo en este caso) necesario para llegar a dicho punto. ¿Simple, correcto? Por desgracia, no. Para cualquier inversa cinemática (IK) ecuación dada, puede haber muchas o ninguna soluciones a un problema dado, y la complejidad de la ecuación aumenta un poco con cada grado de libertad adicional para el sistema. Resolución de ecuaciones de IK requiere un sólido conocimiento de álgebra lineal y hay varias formas diferentes de aplicar la matemática también. Esto es un poco abrumador, así que nos ceñiremos a la aproximación cinemática adelante más apetecible. Cinemática directa nos permite determinar la posición de los puntos del cuerpo en el espacio, dado a la posición de las articulaciones individuales. Puesto que podemos definir la posición angular de los motores, podemos determinar dónde en el espacio 3D es la punta del pincel.
Tiempo de trigonometría!
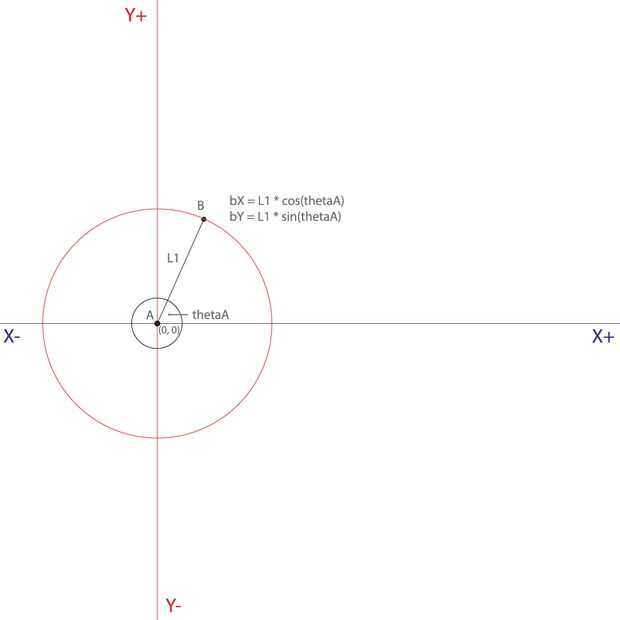
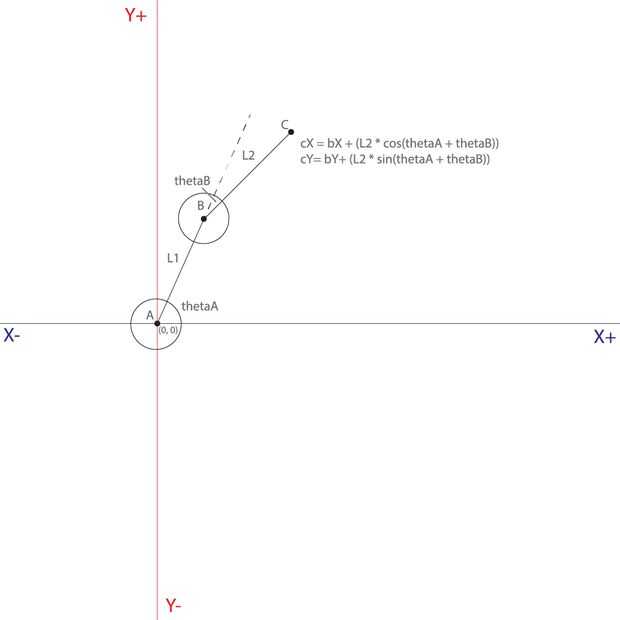
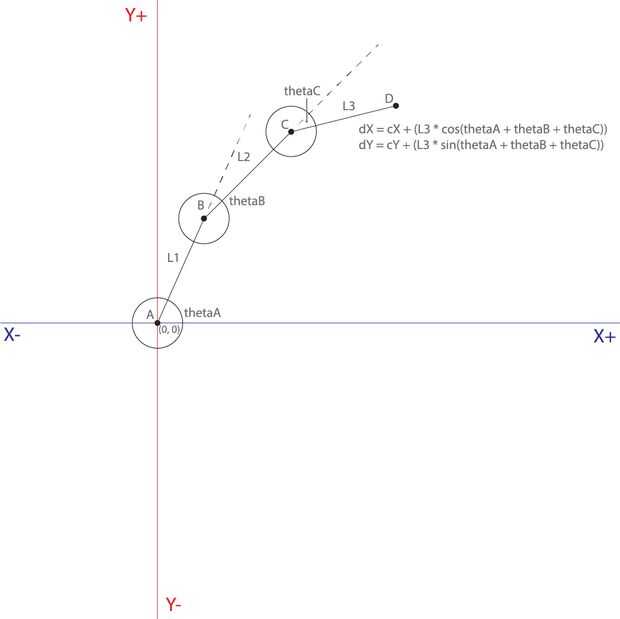
Otro beneficio de FK es que sólo necesitaremos una buena comprensión de la trigonometría para resolver las ecuaciones. Antes de saltar en el espacio 3D, echemos un vistazo a determinar la posición de un punto único, dadas una sola entrada angular. Para empezar, vamos a dibujar un punto A en el origen XY (0, 0). Punto A representa el eje de rotación de motor A (el hombro). El puntal que se extiende desde el motor al eje del motor B es una longitud fija, llamaremos a este segmento de la línea L1. ¿Cómo encontrar la ubicación del punto B, dado el thetaA de ángulo? Utilizando L1 como el radio de un círculo sobre el punto A, podemos encontrar el cartesiano coordenadas del punto B con (X igual a L1 x cos(thetaA) y Y igual a L1 x sin(thetaY). Te queremos trabajar en el espacio de coordenadas Cartesianas, puesto que el lienzo es, en definitiva, un número determinado de puntos en un plano. Dado el punto B y ficha, ahora podemos encontrar punto C. El valor de X del punto C, multiplique la L2 por el coseno de (thetaA + ficha) y luego agregar este valor al valor de X del punto B. El valor Y del punto C, te multiplicamos L2 por el seno de (thetaA + ficha) y luego anuncio esto en el valor Y del punto B. Este patrón se extiende hasta para encontrar el punto D (la punta del pincel), la ecuación de búsqueda que se muestra en el gráfico de la tercera.
La última imagen que ves arriba es la mayor parte de mis notas pensando en esto. Hay muchos artículos sobre cinemática en línea, sin embargo, estos a menudo lanzarse inmediatamente física y explicaciones más complejas para el cálculo de estos datos. Estamos haciendo un robot artístico, no una línea de montaje precisa trabajo-bot, así que vamos a mantener esto simple!