Paso 3: Diferenciarlo!
![]()
![]()
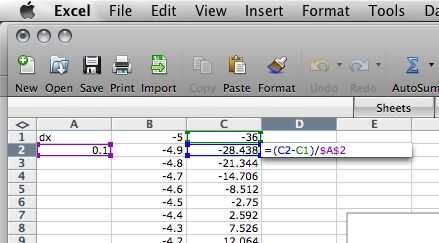
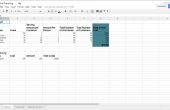
Tramando el derivado es relativamente fácil. Un derivado tiene la forma "dy/dx", en otras palabras, el cambio en y sobre el cambio en x. El cambio en x es fácil y nunca cambia, es a lo que escribimos en la celda A2, que en este caso es 0.1. El cambio y simplemente va a ser la diferencia entre las células, que no es difícil de averiguar. Escriba "=(C2-C1) / $A$ 2' para la celda D2, luego arrástrelo hasta la parte inferior (o haga doble clic en la parte inferior derecha de la celda). El cuadro le dará una buena idea de qué hacer. No habrá nada en la celda D1, distinguiendo perdemos una de las celdas, pero si el dx es lo suficientemente pequeño, no importa. Asegúrese de que escriba esto en D2 en lugar de D1, así cuando se arrastra todo el camino hasta la última celda no mostrar un número ridículamente enorme.
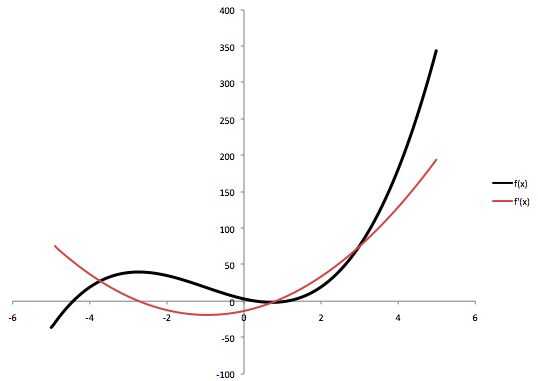
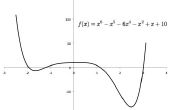
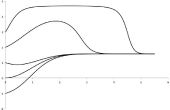
Parcela esta en la misma gráfica como la última de ellas, lo mismo x valores como antes. Es su derivado. También puede hacer el derivado a mano y para asegurarse de que coincida, deben trazar.
Esto es útil si usted está teniendo problemas para diferenciar una función y quieres ver como luce el derivado. Una vez que usted consigue la caída de la diferenciación sin embargo, es bastante fácil y no realmente necesario. Por otro lado, la integración es bastante un poco más difícil, también hay algunas funciones que no sabes integrar. Vamos a hacerlo con hojas de cálculo!