Te acuerdas de la ecuación que determina la salida de un divisor del voltaje,
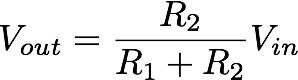
Si esta generalizado para impedancias obtenemos algo así como
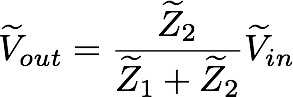
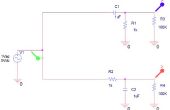
donde Z es sólo la impedancia de los elementos del circuito, y las tildes o líneas onduladas sólo significan nos estamos tratando con números complejos. Para un filtro de paso bajo tenemos una resistencia en la parte superior y un condensador en la parte inferior tan
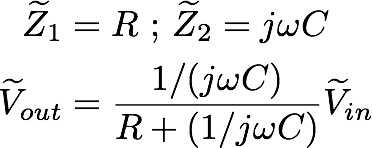
Que es tipo de desagradable aspecto pero si simplificamos obtenemos
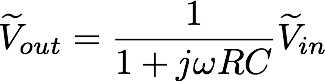
No está demasiado mal ¿verdad?
Esta última fórmula es clave para comprender por qué el paso bajo filtro sólo filtros de alta frecuencia. Observe que para las bajas frecuencias jωRC es aproximadamente cero y así el voltaje de salida aproximadamente igual a la tensión de entrada. Ahora para las frecuencias altas jωRC es aproximadamente infinita y lo que conseguimos la tensión de salida es casi cero. ¿Ver cómo funciona? Cuando nuestra tensión complejo (compuesto de varias ondas con diferentes frecuencias) sirve como la tensión de entrada para nuestro filtro, las piezas de la alta frecuencia de la tensión crean una tensión de salida igual a cero mientras que las piezas de baja frecuencia crean una tensión de salida igual al voltaje de entrada (es decir, que sólo pagarán la parte de baja frecuencia de la señal).
El mismo argumento se aplicó a los filtros de paso bajo puede ser utilizado en filtros de paso alto, sólo tiene que cambiar la ubicación de la resistencia y el condensador. Todavía usamos la misma fórmula
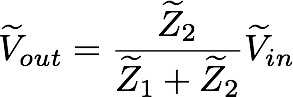
Sin embargo, esta vez
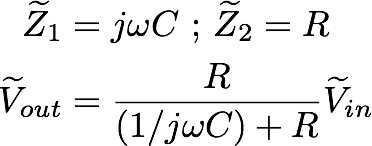
Si simplificamos debemos obtener
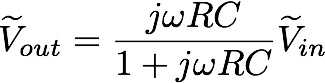
Otra vez, para frecuencias altas básicamente conseguimos jωRC ≈ jωRC + 1 por lo que debemos conseguir una tensión de salida igual a la tensión de entrada. Para frecuencias bajas tenemos jωRC ≈ 0 por lo que la tensión de salida es casi cero. Como puede ver, como había prometido pasamos sobre nuestras frecuencias altas y filtrar sólo la baja frecuencia.