Paso 4: síntesis de circuito lógico

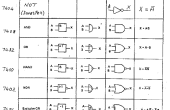
Puertas lógicas pueden ser ensartadas de muchas maneras diferentes. Cada combinación te da una booleana "función diferente." Aquí describiremos dos formas sencillas de diseñar un circuito lógico que resulta en la tabla de verdad exacta que queremos obtener, en este caso mostrado en la tabla.
Suma de productos (SOP)
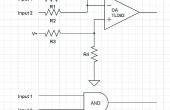
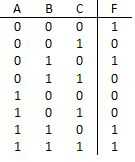
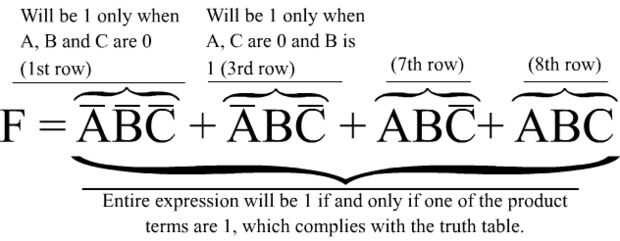
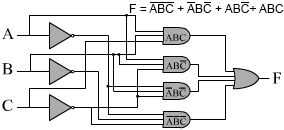
En este enfoque, nos concentramos en las filas de la tabla de verdad que necesitan para producir una salida de 1. Ahora echemos un vistazo a la primera fila. Aviso que si invierta las entradas 0 (todos ellos en esta fila) y multiplicar los juntos (esto se haría con una puerta de entrada de 3 y), tendrá una función que es 1 si y sólo si se cumplen las condiciones de la primera fila: A̅B̅C̅ es 1 sólo cuando A=B=C= 0. Este producto será uno de los términos de nuestros 'suma de productos'. Echemos un vistazo a la siguiente fila donde F= 1 que es la tercera fila. ¿Qué entradas necesitamos invertir para garantizar un valor de 1 cuando ellos se multiplican juntos? A y C son cero, por lo que debe invertirse. El resultado es A̅BC̅, que será el segundo término en la suma. De la misma manera las líneas séptima y octava nos dan ABC̅ y ABC como nuestros terceros y cuarto términos. Tenga en cuenta lo que sucede cuando añadimos nuestros términos juntos y ajuste F = A̅B̅C̅ + A̅BC̅ + ABC̅+ ABC. Cada uno de estos términos será 1 sólo con un conjunto específico de insumos. Por añadirlos juntos F será 1 cuando alguno de estos términos es 1 y 0 si ninguno de ellos son 1 (foto arriba). Por lo tanto, F es conforme con nuestra tabla de verdad. Ahora sólo tenemos que construir el circuito lógico descrito por la función F. Usted puede encontrar el diagrama del circuito anterior.
Producto de sumas (POS)
El segundo enfoque al diseño de circuitos lógicos es muy similar al ya discutido. Como puede haber adivinado, al utilizar el método de producto de sumas, en vez de suma de productos, multiplicamos cantidades.
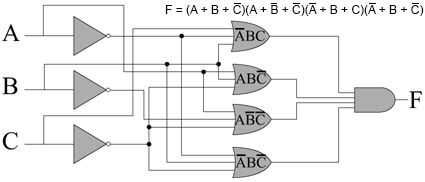
En vez de buscar en las filas de la tabla de verdad con un resultado de 1, nos fijamos en aquellos con un resultado de 0. Echemos un vistazo a la segunda fila. ¿Qué suma producirá un 0 con estas entradas? Si nos invertir C y agréguelas a la A y B, 0 + 0 + 0 = 0. Así que el término para esta fila es A + B + C̅, que es igual a 0 sólo en el caso de la segunda fila. Pasar a la cuarta fila, es obvio que necesitamos invertir B y C, que nos da A + B̅ + C̅. Siguiendo a través de la sexta fila, obtenemos nuestros cuatro términos: A + B + C̅, A + B̅ + C̅, A̅ + B + C, A̅ + B + C̅. Observe lo que sucede si multiplicamos estos juntos: F = (A + B + C̅) (A + B̅ + C̅) (A̅ + B + C) (A̅ + B + C̅). Como alguno de la suma es igual a 0, F será igual a 0. Sólo cuando todos ellos igualan 1 será F igual a 1. Esto cumple exactamente con la tabla de verdad. Una posible implementación de este circuito se da en un diagrama de arriba.
Simplificando
Es obvio que los dos circuitos para la tabla de verdad son bastante complejos, bastante más que lo que necesitan ser. Expresiones de la lógica pueden simplificarse paró mucho, en mucho la misma manera que podría ser simplificado si se tratara de expresiones puramente matemáticas.
Como en Álgebra básica, algunas propiedades se aplican:
- AB = BA
- A(BC) = (AB)C = ABC
- A + B + C = A + (B + C) = (A + B) + C
- A(B + C) = AB + AC
Ya que estamos con álgebra boleana, tenemos algunas propiedades adicionales, que estoy seguro que son bastante intuitivos:
- AA = A
- AA̅ = 0
- A + A = A
- A + A̅ = 1
Una vez que tengas estos simplificación es un pedazo de pastel. Aquí está un ejemplo simple.
Say F = A̅B̅D + A̅BD + BCD + ABC. Si se aplica directamente, sería bastante complejo, que requiere siete puertas para completar este circuito. Vamos a simplificar un poco.
Observe que puede tenerse A̅D fuera el primer y segundo término dándonos F = A̅D (B̅ + B) + BCD + ABC
Desde B̅ + B siempre es igual a 1 cae y nos queda F = A̅D + BCD + ABC
El siguiente paso es un poco más intuitivo. BCD es igual a 1 sólo cuando B, C y D son todos 1. Pero en esta situación cualquier A̅D será igual a 1 o ABC será igual a 1 (comprobarlo). Puesto que además si alguno de los términos es 1 el resultado es 1, el término BCD es completamente redundante y puede descartarse. Esto nos deja con el resultado de F = A̅D + ABC. Esta es una expresión mucho más fácil diseñar un circuito para y puede completarse con sólo cuatro componentes, una mejora enorme! Si tenéis curiosidad puede escribir las tablas de verdad para las expresiones iniciales y finales y ver que son iguales.
A continuación, vamos a poner todo lo hemos aprendido hasta ahora en un gran ejemplo de mundo real!