Paso 5: Final ejemplo
Como un gran final para este Instructable, intentamos combinar todo, desde los pasos anteriores en un ejemplo gigante. Si agarró todo cubierto hasta ahora debería ser relativamente fácil, y si hay todavía uno o dos conceptos no totalmente claro para que luego este ejemplo debe aclarar.
Ha encargado con el diseño del circuito que controla el mecanismo de encendido de una máquina que capsula la pasta de dientes. El circuito debe determinar si o no se enciende la máquina basada en las reglas siguientes:
- La máquina no se enciende a menos que la seguridad ha sido desenganchada.
- La máquina no se enciende a menos tapas de pasta de dientes hayan sido cargados en ella.
- La máquina no se enciende si se ha producido un error o mal funcionamiento.
- Hay un alumbrado que se enciende la máquina independientemente de los casquillos y las advertencias.
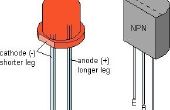
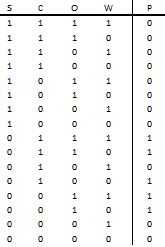
Tenemos cuatro entradas: S es 1 mientras que la seguridad es 0 y en cuando apagado. Entrada C se convierte a 1 una vez que hayan sido cargados todos los tapones. En el caso de cualquier error o mal funcionamiento entrada E se convierte en 1. Entrada O es controlado por el interruptor de anulación manual y es 1 Si enciende. La potencia P se convierte en (1) sólo cuando se satisfacen las condiciones dadas. Lo primero que debemos hacer es hacer una tabla de verdad, así que veamos cómo hacerlo.
Tabla de verdad
Esta parte le será más fácil en lápiz y papel, la tome usted algunos. Ahora dibuje la tabla que has visto hasta ahora en todos los diagramas de verdad y etiquetar las entradas S, C, O y W y la salida del P. El siguiente paso es escribir todas las combinaciones de insumos posibles; ya que tenemos 4 entradas debemos obtener un total de 2 ^ 4 = 16 combinaciones. Una vez hecho esto tenemos que averiguar el resultado de cada juego. Si lo pensamos por un momento podemos reducir drásticamente la cantidad de trabajo requerido. Aviso de las normas que si la seguridad está encendida, la voluntad de la máquina no enciende. Esto significa que cualquier punto S= 1; P= 0. Como la mitad de las salidas se realizan. Vamos a ver el alumbrado a continuación. Para las ocho combinaciones restantes siempre y cuando la anulación es encendido, la salida será 1 independientemente de las otras dos entradas. Cuatro más abajo, debe ser reducido a la mitad otra vez! Ahora echemos un vistazo a los cuatro restantes sistemáticamente. Tenga en cuenta que el orden puede ser diferente en su tabla de verdad según el orden de sus entradas. En mi mesa el siguiente espacio en blanco es donde S C O E igual a 0 1 0 1. Desde E= 1 la salida será 0 (regla 3). Siguiente, cuando S C O E igual a 0 1 0 0 se encuentra que P= 1 porque la seguridad está desactivada, los casquillos se cargan y errores no han ocurrido que cumple con todas las reglas. Pasar a cuando S C O E igual 0 0 0 1. Vemos en la entrada que las tapas no se han cargado todo (regla 2) y se ha detectado algún error o mal funcionamiento (regla 3). Puesto que no ha participado el alumbrado no debe empezar a la máquina en marcha y P= 0. Finalmente el último espacio en blanco es donde todas las entradas son 0. Obviamente las tapas han no se ha cargado otra vez, así que P= 0.
Ahora su tabla de verdad debe ser completa, y usted puede comprobar contra el señalado anteriormente. Una vez más, su pedido puede variar pero las entradas del mismo se debe producir la misma salida. El siguiente paso es encontrar una función que satisface nuestra tabla de verdad.
Diseño de circuito
Aquí tenemos una opción entre el uso de SOP o POS. En la columna de salida vemos muchos 0 pero sólo unos 1. Parece más sencillo utilizar el enfoque de SOP porque entonces tendremos menos términos en nuestra función.
Contamos con cinco líneas con salida de 1. Son: (en el orden S C O W) 0111, 0110,0100,0011 y 0010. Es relativamente sencillo encontrar que la suma de los productos es P = S̅COW + S̅COW̅ +S̅CO̅W̅ + S̅C̅OW +S̅C̅OW̅
Esto es sería un circuito bastante complejo a tratar y construir, así que veamos cómo podemos simplificar las cosas. Obviamente podemos sacar un S̅, y si nos tire CO y C̅O siempre que sea posible obtenemos P = S̅[ CO(W + W̅) + C̅O(W + W̅) + CO̅W̅ ]
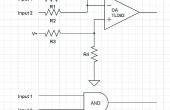
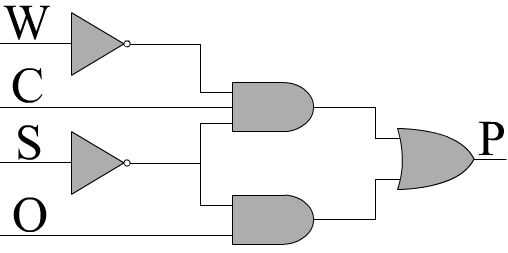
Recordando que una entrada siempre ha añadido a su inversa es igual a 1 (Verifique la identidad de la página anterior), puede rasguñar hacia fuera (W + W̅) y se quedan con P = S̅( CO + C̅O + CO̅W̅ ). Por último, si nos saque O y cero a la resultante C + C̅ término, nuestro resultado será P = S̅O + S̅CO̅W̅. Esto puede ser matemáticamente podemos ir, pero todavía hay una simplificación más que podemos hacer. Ambos términos tienen Oen ellos, uno invertido y otro no. Esto es a menudo una señal de que podemos intentar hacer más simplificación. Vamos a ver si podemos. Obviamente O puede ser 1 o 0. Si es 1 y S̅ también es 1, el término izquierdo será 1 hacer P 1. Si O es 0 y S̅CW̅ = 1, y luego otra vez P = 1. Pero aviso, si S̅, Cy W̅ igualan a 1, entonces P = 1 independientemente de la O. En este caso si O = 1, entonces el primer término será igual a 1 (S̅O = 1), y si es igual a 0 entonces el segundo término es igual a 1 (S̅CO̅W̅ = 1). Por lo tanto nos encontramos con que si S̅, Cy W̅ son 1 O es irrelevante y puede caer de ese término. Esto significa que si la seguridad se ha apagado, los tapones hayan sido cargados y no advertencias son en efecto, la máquina puede encender independientemente de si la anulación manual está encendido o no (Verifique la tabla de verdad y usted encontrará esto es cierto). Ahora, el resultado final es P = S̅O + S̅CW̅, mucho más práctico no es. Arriba se muestra una posible implementación de esta función. Observe cómo algunos componentes usa en comparación con el SOP original empezamos con.
Ahí lo tienen! En el espacio de pocos minutos hemos tomado un problema, encontró una solución, lo optimizado y hemos implementado los resultados. Este Instructable apenas araña la superficie de las maravillas de la electrónica digital, pero que han ganado una comprensión básica y un agradecimiento para él. Entonces esto concluye el Instructable, espero que te ha inspirado para diseñar y hacer algo de su propia.