Paso 4: Pendiente - intercepción método fórmula
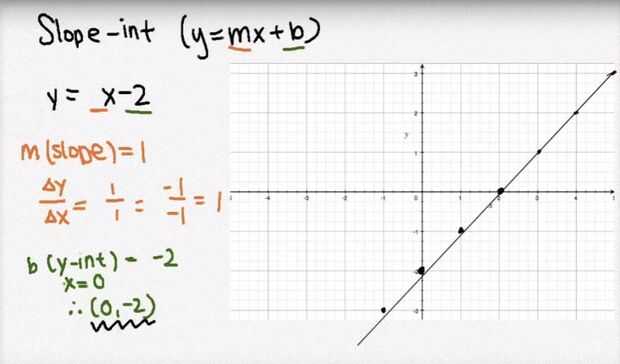
Para el método de la ecuación, es necesario primero reordenar la ecuación en la forma y = mx + b. Entonces puede parcela b, la intersección y encontrar otros puntos con m, la pendiente. En mi opinión, este método es el más eficiente, especialmente si la ecuación está ya escrita en la forma pendiente-intercepto.
- Reorganizar la ecuación en la forma pendiente-intercepto, y = mx + b. En el problema anterior, y = x-2 estaba ya en la forma pendiente-intercepto, por lo que no debemos hacer nada para este paso.
- Encontrar b, la intersección y marca el punto en el gráfico. En este caso, la intersección es -2 por lo que debemos trazar el punto (0, -2).
- Encontrar m o la pendiente. Puesto que la pendiente es el cambio en y sobre el cambio en x (o aumento de plazo), podemos trazar el punto siguiente mediante el uso de la pendiente. En el problema del ejemplo, la pendiente es 1, que equivale a 1/1. Así que el cambio en y sobre el cambio en x es 1 sobre 1. Esto significa que de la intersección (0, -2), debemos avanzar una unidad y una unidad hacia la derecha para encontrar otro punto en el gráfico. Esto nos lleva a (1, -1). Seguimos repitiendo por subir una unidad y una unidad hacia la derecha. Una vez que tenemos suficientes puntos, podemos conectar los puntos y crear la línea.
- Nota: Subir 1 unidad, 1 unidad a la derecha no es la única opción. En el problema de la práctica, la pendiente es 1, que también es igual a-1 /-1, 2/2, 3/3, etc.. Así que podemos utilizar cualquiera de estas fracciones la línea de la gráfica. Por ejemplo, si elegimos utilizar-1 /-1, podemos mover una unidad y una unidad hacia abajo a la izquierda de la intersección. De cualquier manera, todavía tenemos la misma línea.