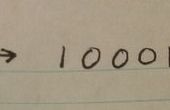Paso 2: Base de conceptos básicos (continuación): binario

Como su nombre indica, un binario sistema de numeración consta de dos números: 1 y 0. Por consiguiente, esto se refiere como base 2 y los números parecen 100100102. En tal sistema, la representación de valores se logra a través de un sistema de "poder de dos". Cada lugar en un número binario, refiere a menudo como un poco, tiene un valor particular que puede ser fácilmente determinado. Números binarios se suelen escribir como un múltiplo de ocho, o un byte. A veces, se utilizan sólo cuatro bits del byte, o la mitad superior o inferior y estos cuatro bits se denominan colectivamente un nibble. Nibbles se vuelven importantes cuando conversión entre bases, como se verá más adelante.
Sin digressing, utilizaré la notación endian grande donde números enteros se almacenan en memoria empezando por el bit más significativo (MSB) y terminando con el bit menos significativo (LSB). La ubicación de valor de cualquier dado de bits es determinada tomando dos (el número de dígitos en el sistema binario) a la potencia de la broca del lugar utilizando un índice de base cero: 2 bits. Por ejemplo, el LSB de la nibble es 20 ó 1. El cuarto bit, es decir, el tercer lugar (recuerda empezar en cero) valor es 23 o 8. Veamos sólo algunos ejemplos para hacerlo más claro. Aquí es cómo un nibble es representado en binario.
Zero-based index 3 2 1 0 Bit place 4th 3rd 2nd 1st Bit value 8 4 2 1 Example values: Decimal 12 1 1 0 0 Decimal 5 0 1 0 1
Si el valor de bit debe ser añadido (o cuenta) ese bit será un 1, otra cosa será un 0. Sabiendo esto, el valor decimal de "1" se escribe "0001", porque el bit 1 y ese valor es uno. El valor decimal de "10" se escribe en binario como "1010" y si añades los bits de valor donde hay un 1 luego verá lo añade a 10. De esta manera, un nibble puede representar los números 0 a 15. Números más grandes requieren el uso del nibble de orden alto.
Bit place 8th 7th 6th 5th 4th 3rd 2nd 1st Bit value 128 64 32 16 8 4 2 1 Example value: Decimal 88 0 1 0 1 1 0 0 0 Decimal 253 1 1 1 1 1 1 0 1
Agregar los valores de bit para cada bit del lugar que tiene un 1 para satisfacer a ti mismo que los valores decimales con precisión están representados por el valor binario a la derecha.
Cubriré de adición binaria, resta, multiplicación, división, puntos flotantes y números negativos a través de 2 complemento y 1 de complemento en un instructable después ya he empezado trabajando en llamado Cómo calcular como un microcontrolador, pero aquí está una vista previa como una tentación (sí, como matemáticas binario pueden ser un incentivo, derecha?) a ve y vota mi instructables otros. :)
Vista previa de Cómo calcular como un microcontrolador .
Aritmética binaria: Suma y resta
Aritmética binaria es muy simple y directa. Debe familiarizarse con la representación binaria de números de cero a tres, si no tienes estas comprometido al corazón. Son 00, 01, 10 y 11. Lo principal a recordar es llevar sobre unos y que es lo más difícil que tendrá que hacer, así que respirar tranquilos.
Voy a añadir 15810 y 5110 en binario, que si ya ha agregado los rendimiento 20910. Seguir y comprobar mis cálculos.
1001 1110 + 0011 0011 -------------
Ahora, agregar abajo de la LSB (derecha) hacia la izquierda. La primera es 0 + 1 que es 1. El siguiente es 1 + 1 es 2, pero en binario es 10. Se trata de dos dígitos, así que tenemos que llevar eso a la siguiente columna.
1001 1110 + 0011 0011 ------------- 01 ------------- 1
En la columna, es 1 + 0 + 1, que es otra vez dos, o 10. Llevar eso. Continuar.
1001 1110 + 0011 0011 ------------- 0001 ------------- 1111
Ahora tenemos 1 + 1 + 1 que es tres, o, sí, ya lo tienes: 11. Así que en vez de poner un cero y llevando a 1, poner un 1 y llevar uno. Continuar hasta el final.
1001 1110 + 0011 0011 ------------- 1101 0001 ------------- 111111
El 110100012 es 20910, así que hicimos nuestros cálculos correctamente.
Aritmética binaria: Multiplicación y división
En el sistema de base 2, división y multiplicación por una potencia de dos se logra fácilmente por derecha e izquierda, desplazamiento, respectivamente. Desplazamiento es exactamente como suena: cuando salió de cambio por n, tener todos los de 1 y 0 y moverlos números lugares a la izquierda en los lugares cambiados de puesto con 0. Cuando lógicamente adecuada cambio por lugares números, mueves el binario valores números lugares a la derecha, llenar las ranuras movidas con 0 (hay también una cambio derecha aritmética, pero no lo cubro aquí). En el ejemplo siguiente, cambiar el número 4 a la izquierda un poco. El bit #1 es el 2 º de derecho en nuestro sistema de índice de base cero, y también podemos escribirlo 21 o 2. Esto debe causar una multiplicación de 4 * 21 o 8.
Left shift: 4 << 1 Bit value: 8 4 2 1 Binary: 4 = 0 1 0 0 Shifted to the left one bit: 1 0 0 0 = 8 denary
Puedes ver cómo cambiar a la izquierda cambia el número de cuatro a ocho, con eficacia multiplicando el valor por dos. Nosotros podríamos también cambiar izquierda por dos bits o cualquier número de bits de 1 hasta n - 1, donde n es el número de bits en nuestro número binario. En consecuencia, cambiando un binario número a la derecha divide con eficacia el número por una potencia de dos. Pensar si no está claro a continuación, echa un vistazo a continuación. Aquí nos cambiar dos de 32 bits a la derecha, efectivamente dividiendo 32 por 22 , rendimiento de 8.
Right shift: 32 >> 2 Bit value: 128 64 32 16 8 4 2 1 Binary 32 = 0 0 1 0 0 0 0 0 Shifted to the right two bits: 0 0 0 0 1 0 0 0
Que está lejos de todas las operaciones binarias fundamentales, pero es una cobertura adecuada para nuestra lil' ' ol instructable aquí.