Paso 7: Factorización polinomios agrupando
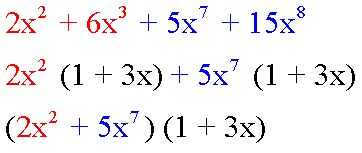
2 x ^ 2 + 6 x ^ 3 + 5 x ^ 7 + 15 x ^ 8
Hay ningún coeficiente común y Factorizando por x ^ 2 no ayuda mucho. Esto es donde utilizas agrupación al factor.
Agrupación: factoring al GCF de sólo dos términos de la expresión. Se puede ver que 2 x ^ 2 + 6 x ^ 3 y 5 x ^ 7 + 15 x ^ 8 ambos puede tener un GCF sacado. Hacerlo.
2 x ^ 2 (x 1 + 3) + 5 x ^ 7 (1 + 3 x)
Tenga en cuenta que hay un factor común, 1 + 3 x. Esta expresión puede ser reformulada a (2 x ^ 2 + 5 x ^ 7) (x 1 + 3). Allí está tu respuesta.
Tenga en cuenta que (2 x ^ 2 + 5 x ^ 7) (x 1 + 3) se puede factorizar más Factorizando fuera una x ^ 2 en el primer binomio: x ^ 2 (x 2 + 5 ^ 5) (x 1 + 3).