Paso 8: Factorización de polinomios por división sintética
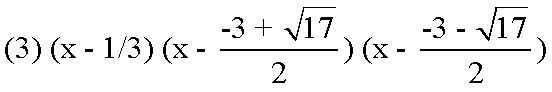
x 3^ 3 + 8 x ^2 - 9 x + 2 es un ejemplo. Se puede utilizar agrupación al factor hacia fuera un GCF de manera que se produciría un factor común.
Para explicar como funciona esto, necesita saber que al solucionar una ecuación por factorización, necesita establecer lo factorizado hacia fuera igual a 0 y averiguar lo que X es igual a que es igual a cero. Por ejemplo, 0 = (x - 2) (x + 1). Las soluciones son 2 y -1.
Si un polinomio tiene coeficientes enteros, cada cero, o solución, tiene la forma P/Q, donde P = un factor del término constante y Q = un factor del coeficiente principal.
Básicamente, si una lista de todos los factores de la constante y dividir por los factores del coeficiente principal (el coeficiente junto a la variable con el poder más alto) en cada combinación, usted conseguirá una lista de posibles soluciones racionales. ¿Cómo esto ayudará factor? Si tiene 2 como una solución, puede trabajar hacia atrás y decir que fue uno de los factores de la ecuación (x - 2).
Así, el ejemplo:
Factores de 2: + /-1 +-2 (es necesario incluir negativos)
Factores de 3: + /-1, +-3
P/P: + /-1 +-1/3, +/-2, +/-2/3
Una vez tengas tu lista, a usar algo llamado división sintética para ver cuáles de aquellos P/Q son realmente soluciones.
La división sintética es una forma de dividir polinomios por un binomio de la forma x-k. No voy a explicar cómo funciona, sino simplemente mostrar cómo utilizar para factoring.
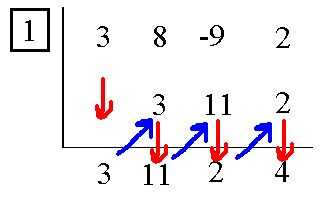
En primer lugar, poner uno de su P/Q en una pequeña caja o paréntesis, luego los coeficientes y constantes en una fila al lado de la lista. Si el polinomio salta una potencia (x^ 2 + 2) y luego tienes que añadir un 0 donde x1 debería haber sido.
(Expresión: 3 x ^3 + 8 x^ 2 - 9 x + 2)
(Omitir los asteriscos, se utilizan como marcadores de posición. Mejor aún, ver la primera foto.)
(1) 3 8 2-9