¿Como factor de (2 / 20 paso)

Paso 2: Teniendo el GCF de una expresión

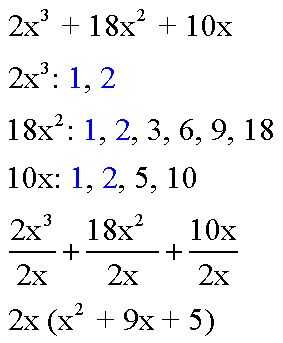
Expresiones algebraicas constan de números, llamados coeficientes, y las variables, que pueden ser elevadas a una potencia. En la expresión x^{^ 2} + 6 x + 8, 1 es el coeficiente de x^{^ 2}, la variable. (Si no ves un coeficiente antes de una variable, es un 1, porque x ^² se multiplica por 1.) Asimismo, 6 es un coeficiente de x^{^ 1}. (Una única variable está elevada a una potencia de uno). 8 se llama una constante - no es multiplicado por una variable. (Usted puede visualizarlo que multiplicado por x^{^ 0}, y cualquier número elevado a la potencia 0 es igual a 1).

Para factor de una expresión, se tiene que empezar Factorizando la GCF o máximo común divisor. Lista de los factores de cada componente de la expresión. Aquí estamos interesados en encontrar los factores del número natural.

La expresión x^{^ 2} + 6 x + 8 tendría factores que este aspecto:

x^²: 1
x 6: 1, 2, 3, 6
8: 1, 2, 4, 8

Si nos fijamos en las tres listas, hay sólo una cosa que comparten en común, el número uno. Esto significa que no hay coeficiente mayor que uno el factor hacia fuera.

Entonces nos fijamos en las potencias de los exponentes. 2, 1 y 0. Si aparece un cero, la expresión no puede tenerse por una variable.

Esta expresión está lista para el siguiente paso.

Aquí hay un ejemplo que tiene un GCF que debe tenerse hacia fuera: 2 x^{^ 3} + 18 x^{^ 2} + 10 x. Factor de cada parte:

2x^{^3}: 1, 2
18x^{^2}: 1, 2, 3, 6, 9, 18
x 10: 1, 2, 5, 10

Aquí podemos ver que las piezas tienen 1 y 2 en común. Nos encontramos con el mayor número, 2.

Entonces nos fijamos en las potencias de exponentes: 3, 2 y 1. encontrar el menor número que no sea 0, en este caso el número uno. Que significa x^{^ 1}, o simplemente x, se puede dividir en la expresión.

Multiplicar el número y la variable a para obtener x 2. Luego divida cada parte de la expresión por x 2.

2x^{^3} / 2x = x^²
18 x^{^ 2} / 2 x = 9 x
10 x / 2 x = 5

La expresión con el mcd factorizado a es 2 x (x ^² + 9 x + 5). Tenga en cuenta que debes poner la expresión factorizada en paréntesis y escribir el GCF junto a él.