Paso 4: Factorización de trinomios
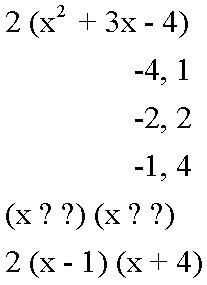
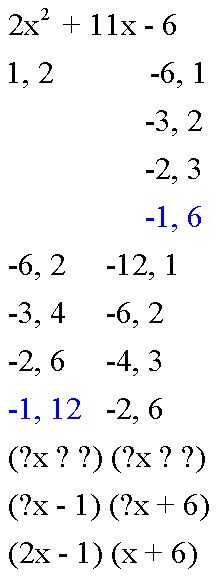
Factor primero, por el GCF. Esta siempre será su primer paso cuando cualquier expresión de factoring.
2 (x ^2 + 3 x - 4)
Si terminas con una potencia de x mayor que dos después de factoring al GCF, pasar a otro paso.
Lista de los factores del número entero de la constante. Tendrás dos sincronizarlos como así:
-4, 1
-2, 2
-1, 4
Usted quiere encontrar uno de estos que cuando sumados es igual al coeficiente del segundo término, 3. -1 + 4 = 3. Desde aquí, escriba dos grupos de paréntesis con x dentro:
(x) (x)
Luego se pegan los dos términos que en el paréntesis.
(x-1) (x + 4)
No te olvides de añadir el GCF nuevo.
2 (x - 1) (x + 4)
Es cómo el factor de un trinomio.
Aquí es otra: 2 x^ 2 + 11 x - 6.
Hay un giro esta vez: el coeficiente de x^ 2 no es 1. Esto significa que estaremos agregando otro paso:
Lista de factores de la constante, -6, así como el coeficiente de x2, 2.
-6, 1
-3, 2
-2, 3
-1, 6
1, 2
Ahora, querrás multiplicar cada uno de los factores a la izquierda por 1 y a la derecha por 2. Repetir cambiando el 1 y 2. Terminarás con
-6, 2
-3, 4
-2, 6
-1, 12
-12, 1
-6, 2
-4, 3
-2, 6
Encontrar la pareja que se suma al coeficiente del término medio, en este caso, -1 + 12 = 11. Configurar los paréntesis:
( x ) ( x )
Palo en los números originales (que tenía antes de multiplicar por 1 y 2):
(x-1) (x + 6)
Luego pegar en el uno y dos como los coeficientes de x para que al multiplicar los términos internos y externos y agregarlos juntos, obtendrás 11.
(2 x - 1) (x + 6)
Si revisas tu trabajo por frustrar él hacia fuera, usted terminará con x 2^ 2 + 11 x - 6, la expresión que usted comenzó con. ¡ Felicidades!