Paso 1: Principio del circuito de funcionamiento
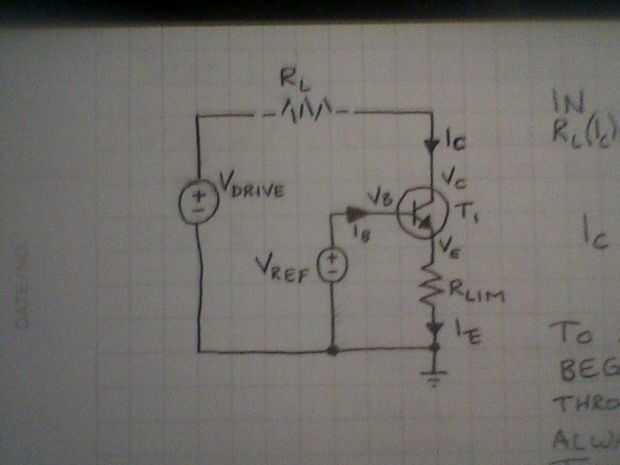
El circuito mostrado es un sumidero de corriente regulado. Puede ser un elemento útil en sus proyectos futuros. Regula la corriente a través de [L], evitando que se exceda un valor determinado. Sin embargo, este circuito no tiene la capacidad de la unidad activa, y así debe ser lo suficientemente grande como para conducir la corriente deseada a través de [L] V [unidad].
La corriente a través de [L] es igual a I [C]. [C] es aproximadamente igual a V [REF] - (V [ser] de T1) / R [LIM].
Para ver donde se origina esta ecuación, empezaré señalando que la suma de los voltajes alrededor del lazo formado por V [REF], la Unión base-emisor de T1 y R [LIM] debe ser cero (por ley de voltaje de Kirchhoff):
V [REF] - V [SER] - V [RLIM] = 0
por lo que
V [RLIM] = V [REF] - V [SER].
La corriente a través de R [LIM] (también conocido como I[E]) se define por ley de Ohm, y podemos sustituir utilizando la ecuación anterior:
I [E] = V [RLIM] / R [LIM] = (V [REF] - V [SER]) / R [LIM].
Haciendo caso omiso de la corriente de base,
QUE [C] = I [E],
por lo que la corriente por la resistencia de carga es aproximadamente definida por
YO [CARGA] = I [C] = (V [REF] - V [SER]) / R [LIM].
Si desea incluir los efectos de la corriente base del transistor, debe también factor en la ganancia de corriente del transistor, h [FE].
Viendo el transistor como un nodo, por la ley actual de Kirchhoff,
0 = I [C] + [B] - QUE [E]
por lo que
I [B] QUE [E] - I [C].
Sabemos que h [FE] es el factor que podemos multiplicar por I [B] para encontrar nuestro yo [C]. Por lo tanto,
I [B] * h [FE] = I [C].
Sustituir por I [B] de la ecuación anterior,
(I [E] - I[C]) * h [FE] = I [C].
Resolviendo para I [C],
Que [C] = [E] - I (I [E] / (1 + h [FE])),
y desde que [E] = (V [REF] - V [BE]) / R [LIM],
la exacta ecuación entonces queda:
Que [C] = ((V [REF] - V [BE]) / R [LIM])-(((V [REF] - V [BE]) / R [LIM]) / (1 + h [FE])).