Paso 1: Matemáticas: conversión de posición de la pluma a ángulos de servo
Esta sección explica cómo la posición del cursor del ratón en la pantalla de la computadora se convierte en ángulos de los servomotores para que al final de la escritura de los brazos articulados replica el movimiento del cursor del ratón.
No es necesario comprender esto para llevar a cabo la intructable, proporcionará las piezas de código que implementa la conversión de la posición del cursor a los ángulos del servomotor.
Analizar un solo servomotor
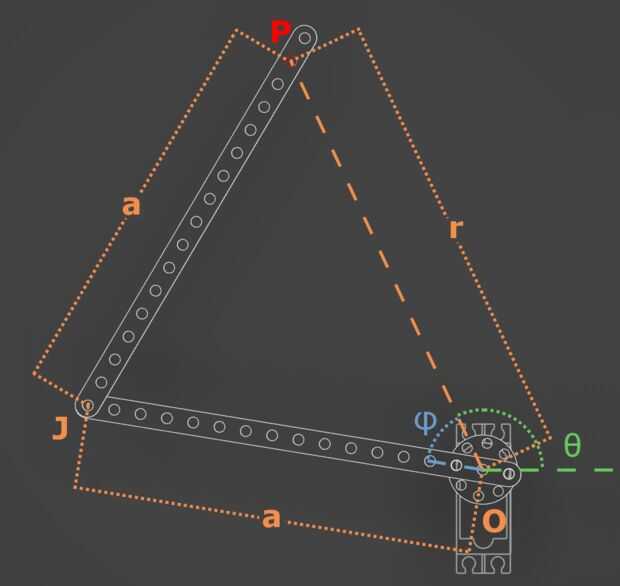
Si analizamos una configuración con un solo brazo y un servomotor (figura anterior):
Llame O el origen de nuestro referencial. Se coloca en el eje de rotación del servomotor.
Llame P el punto que queremos alcanzar en el plano de la escritura, o posición de la pluma.
Llame a (x, y) las coordenadas de P.
Llame a la longitud de los segmentos de brazos. (Nota: si todos los segmentos del brazo son de igual longitud, los cálculos son mucho más fáciles).
Llame a J la posición de la articulación donde se conectan los segmentos de dos brazos.
Llame a r la distancia OP: r = (x ² + y²)1/2
Llamar θel ángulo entre el OP y el eje x: θ = atan2(y,x)
En el triángulo OJP:
La distancia OJ = un
La distancia JP = un
Llame a φ el ángulo PÔJ : φ = acos (r / (2a))
Llamada α el ángulo que debe alimentar el servomotor para llegar a la posición P:
α = θ + φ
Α = atan2(y,x) + acos ((x ² + y²)1/2 / (2a))
Tenga en cuenta que este ángulo de alimentación a un único servomotor no limitará la posición de la pluma a un punto. Limitará a J a un solo punto pero dejará libertad para moverse en un círculo de radio a alrededor de J. agregar que el segundo servomotor nos permitirá limitar la posición de P más P.
Agregar el segundo servomotor
Podemos repetir el cálculo hecho en el párrafo anterior, excepto que esta vez el punto que queremos llegar a P, se ve en el referencial del segundo servomotor, que es un desvío desde el referencial hemos utilizado antes.
Llame a d la distancia entre los ejes de los dos servomotores.
Las coordenadas de P en el referencial del segundo servomotor son: (x + d, y)
La configuración de los brazos del segundo servomotor es similar pero refleja, por lo que encontramos:
Llamar α2 el ángulo que debe alimentar el segundo servomotor para llegar a la posición P:
α2 = θ2 - φ2
Α2 = atan2(y,x+d) - acos (((x+d) ² + y²)1/2 / (2a))
Alimentación de los ángulos α y α2 dos servomotores limitará P en la intersección de dos círculos = dos puntos. Podemos restringir el dominio de P de tal manera que la pluma se colocará inicialmente en la parte superior de estos dos puntos y nunca tiene la oportunidad de cambiar a otro punto de intersección.
De esta manera podemos controlar completamente la posición de la pluma alimentando dos ángulos para los servomotores.
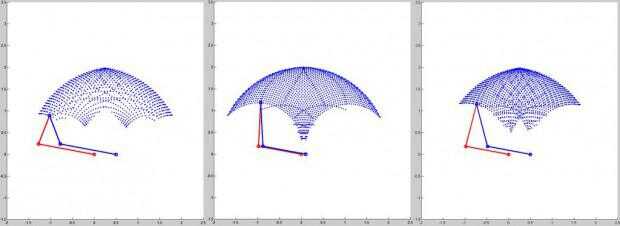
Las imágenes de arriba muestran las formas del dominio accesible en el plano de la escritura para diferentes valores de la longitud del brazo (a) y el servomotor desplazamiento (d).













