Conversión de decimales a números binarios (3 / 5 paso)

Paso 3: Contar en binario con decimales (parte 2/2)

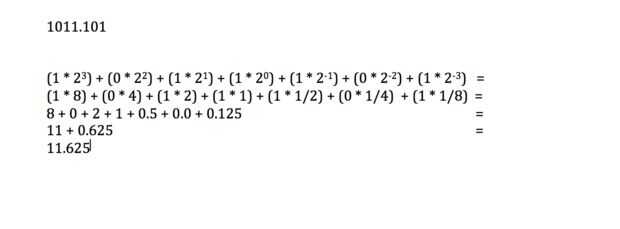
Ahora que usted entiende cómo contar números binarios que son enteros (números enteros), también tienes que entender cómo contar números binarios que tienen decimales (no enteros). Los siguientes son ejemplos de números enteros y números no enteros en base 10. A "|" se utiliza para separar cada número en la lista.

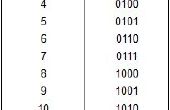
Números enteros:

(Base 10) -> 19 | 102 | 72 | 9212 | 8

(Base 2) -> 0010 | 0111 | 1111 | 1000

No enteros:

(Base 10) -> 14,7 | 18.2 | 19.5 | 25.4

(Base 2) -> 1011.101 | 0011.11 | 101.011

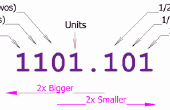
Observe cómo los números no enteros utilizan decimales. Para encontrar el valor de cada dígito que está a la derecha de un punto decimal, utilizar poderes negativos para representar la posición de cada número. Para entender más esto, echa un vistazo a otro ejemplo.

Ejemplo

1011.101

Comience contando la parte del número que está a la izquierda del punto decimal y luego mover a la derecha del punto decimal. Los dígitos en negrita representa cada dígito que trabajamos para ese paso. Base 2 en todos los pasos tan 2 sirven como el multiplicador que se eleva a la potencia de la cifra actual en esa posición.

1011. 101 -> aquí, el dígito 1 está en la posición cero, por lo que esta cifra equivale a 1 * 2 ^ 0 = 1

1011.101 -> aquí, el dígito 1 está en la posición uno, por lo que esta cifra equivale a 1 * 2 ^ 1 = 2

1011.101 -> aquí, el dígito 0 está en la posición dos, por lo que esta cifra equivale a 0 * 2 ^ 2 = 0

1011.101 -> aquí, el dígito 1 está en la posición tres, por lo que esta cifra equivale a 1 * 2 ^ 3 = 8

Sumar estos números por rendimiento la respuesta 11.

Ahora hacia la derecha de los decimales. Cuando cuenta la izquierda del punto decimal, la posición comienza en 0. Cuando cuenta el lado derecho, la posición iniciar en 1 e incrementar en 1 en cada posición. Otra cosa diferente es el multiplicador en cada posición. El multiplicador es ahora una fracción con el número 1 está constantemente el numerador (valor en la parte superior de la fracción) y el multiplicador es ahora el denominador (el valor en la parte inferior de la fracción). Por lo que el multiplicador para el primer dígito inmediatamente a la derecha el multiplicador sería (1/2 ^ 1) que es igual a (1/2), la siguiente sería (1/4), seguido por (1/8), seguido por (1/16)... y así sucesivamente en potencias de 2.

Pasando a la derecha del punto decimal ahora, usted puede averiguar lo que el valor real del número binario está empezando con el primer número a la derecha del punto decimal. Una calculadora también se recomienda para esta parte porque se trata de conversión de fracciones a decimales.

1011.101 -> aquí, el dígito 1 está en la primera posición a la derecha del punto decimal, así que tenemos: 1 * (1/2) = 0.5

1011.101 -> aquí, el dígito 0 está en la segunda posición a la derecha del punto decimal, así que tenemos: 0 * (1/4) = 0.0

1011.101-> aquí, el dígito 1 está en la tercera posición a la derecha del punto decimal por lo que tenemos: 1 * (1/8) = 0.125

Ahora sume el valor de cada dígito resultante para encontrar el valor real de decimal. 0,5 + 0.0 + 0.125 = 0.625.

Usando la respuesta de 11 para el lado izquierdo de la decimal y nuestra respuesta de 0,625 para la derecha de los decimales, encontramos que nuestra respuesta final es 11.625