Paso 2: XOR no binario, bit a bit no

Así que la pregunta es puede este tipo de cosa trabajar con cifras y no sólo a nivel binario. Creía que podía así que intenté resolver en mi cabeza y en el papel. Esto es lo que pensé sería el resultado de base10.
A xor B = C--> C xor B = A--> C xor A = B
0123456789--> 10 dígitos
10-9 = 1-3 =-2--> 3 xor 9 = 8--> 8 xor 9 = 3
10-8 = 2-3 =-1--> 3 xor 8 = 9--> 9 xor 8 = 3
10-7 = 3-3 = 0--> 3 xor 7 = 0--> xor 0 7 = 3
10-6 = 4-3 = 1--> 3 xor 6 = 1--> 1 xor 6 = 3
10-5 = 5-3 = 2--> 3 xor 5 = 2--> xor 2 5 = 3
10-4 = 6-3 = 3--> 3 xor 4 = 3--> xor 3 4 = 3
10-3 = 7-3 = 4--> 3 xor 3 = 4--> xor 4 3 = 3
10-2 = 8-3 = 5--> 3 xor 2 = 5--> 5 xor 2 = 3
10-1 = 9-3 = 6--> 3 xor 1 = 6--> 6 xor 1 = 3
10-0 = 10-3 = 7--> 3 xor 0 = 7--> 7 xor 0 = 3
Por supuesto mis matemáticas no funcionan muy bien para la codificación en el ordenador. Por el contrario debe ser posicional basado en un conjunto. El conjunto es el alfabeto por lo que-para-hablar. La longitud del alfabeto y la posición de los partidos son los factores importantes para la codificación. Vamos a ver si podemos hacer una versión binaria para probar la teoría. Así que en binario, el alfabeto es fácil "0" y "1".
Set = "0" "1"
Longitud = 2
Max = 1
¿A = 1, B = 1, C =?
Max - position1 - postion2 = position3
1 - 2 - 2 = -3
Oh, oh! ¿-3? Decidí que la solución más fácil a esto es comprobar un número entero no positivo y escribir el valor como estaba contando hacia atrás sin remanente o resto.
En este ejemplo binario sólo puede haber dos posiciones "1" y "2".
Si agrego la longitud del conjunto que es 2 -3 -1 se trata, agrega longitud otra vez y tenemos 1. Sobre esta base se evaluaría 0 y -2 a la posición 2.
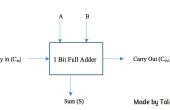
Con estas condiciones en el lugar esto funcionará para emular la tabla de verdad de un XOR bit a bit:
A(in) POS(a) B(in) POS(b) C(out) POS(c)
0 1 0 1 0 1
1 2 0 1 1 2
0 1 1 2 1 2
1 2 1 2 0 1
.