Paso 1: Gausiano vs media curvatura... ¿Es desarrollable?
Con el propósito de este instructable, voy a suponer que trabajamos con un material rígido con mínima flexibilidad y plasticidad (como madera, papel, acrílico, etc.) por lo que sólo se ocupan de superficies desarrollables. Es posible crear superficies no desarrollables (o doblemente curvada) con bisagras enrejado ampliando el patrón, pero esto sólo es posible con materiales flexibles (metales y plásticos) y es una conversación mucho más grande sobre geometría (consulta de Daniel Piker blog).
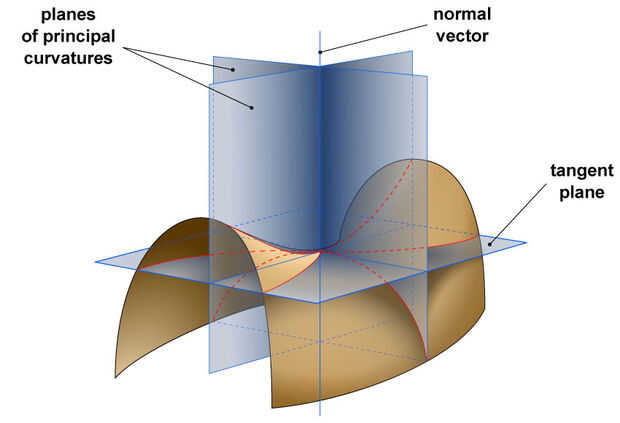
Entonces, ¿qué es una superficie desarrollable? Es una buena pregunta. Una superficie desarrollable es uno que sólo tiene curvatura en una dirección. ¿Qué significa eso? Pregunta aún mejor. Encontré un artículo que lo explica bien aquí http://brickisland.net/cs177/?p=144. "Superficie con cero curvatura Gaussian se llama superficies desarrollables porque pueden ser"desarrollados"o aplanados hacia fuera en el plano sin estiramiento o desgarro. Por ejemplo, cualquier pieza de un cilindro es urbanizable ya que una de las curvaturas principales es cero". Básicamente, si escoger un punto en una superficie y se cruzan la superficie con un plano en ese punto, da la curvatura de principio en una dirección. Si usted intersecan la superficie con otro plano perpendicular a la primera, le da la curvatura de principio en la segunda dirección. Curvatura media es el promedio de las curvaturas de dos principio y curvatura Gaussian es el producto de las curvaturas de dos principio. Las superficies desarrollables son definidas por superficie con cero curvatura Gaussian.
(Imagen de Wikimedia Commons)











