Paso 2: DAC cargado binario

• discutir, construir y modificar un DAC cargado binario
• identificar los componentes de un DAC cargado binario
• crítica y evaluar las deficiencias de este diseño

El DAC cargado binario

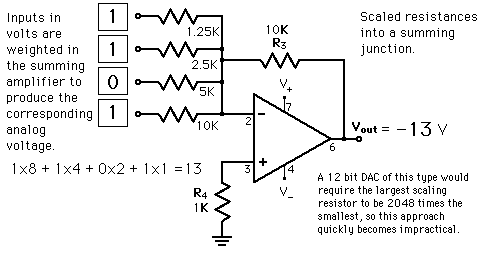
La figura incluida a continuación en esta sección se muestra un simple binario-weighted DAC construye conmutadores digitales (podría ser de un IC 4066 o interruptores individuales separados) y un conjunto de resistencias ponderadas conectado a un amplificador operacional. El amplificador operacional crea un amplificador inversor resistencia sumas de entrada R_en a través de un circuito de retroalimentación de R₃. Los interruptores y resistencias actúan juntos como una resistencia controlada digitalmente que puede tomar una de 16 valores diferentes de resistencia. Esencialmente, esto proporciona una fuente de corriente controlada digitalmente. Cada nuevo código binario aplicado a las entradas genera un nuevo nivel actual discreto que se suma por R₃ para proporcionar un nuevo nivel de tensión de salida discreta.

Aquí, los valores de resistencias son R, R/2, R/4 y R/8 donde R = 10 K ohm y R₃ = 10 K ohm. El circuito equivalente del amplificador op genera V_a = -V_en(R3/r_en) = - 5 v (10 K/R_en) con una entrada de 5V. Para encontrar todos los valores posibles de R_en podemos usar el fórmula de estándar "resistencias en paralelo" de:

1/R_en = un 1/8R + B 1/4R + C 1/2R + D 1/R

Aquí la A la D actuar como un coeficiente binario de modificar la resistencia en el lugar apropiado del binario. Para encontrar el voltaje de salida analógico, simplemente utilizas la fórmula ya incluí arriba:

V_out = -V_in(R₃/R_in)

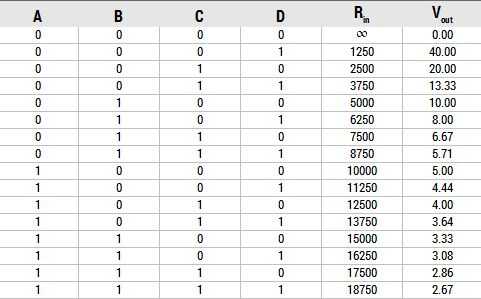
Suponiendo que V_en de 5V y₃ de la R de 10 K, vienen para arriba con la tabla incluida a continuación.

Este DAC cargado binario está limitada a 4 bits de entrada generando 16 pasos de salida analógica. Al doble de la resolución, se podría pensar en cuatro resistencias más en 1/16R, 1/32R, 64R/1 y 1/128R y sería correcto... pero sólo parcialmente. Esto es donde la aplicación incumple teoría. El problema con este enfoque es que cuando llegas a la resistencia de 1/128R, usted tendría que encontrar una resistencia de ohm 78,125 y aunque encontró uno, o uno había construido a partir de resistencias independientes, usted seguiría siendo plagado con nivel de tolerancia de la resistencia. Una tolerancia del 10% significa que el valor real de la resistencia de ohm 78,125 puede fluctuar dentro de +-10%. Se puede hacer mejor con una resistencia de 1% de tolerancia pero, ¿cómo llegar 3 cifras significativas de la resolución?

Este enfoque binario/escala ponderada nos falla cuando necesitamos más de pocos bits de resolución. ¿Qué debemos hacer? Este diseño de basura y dar vuelta la página!