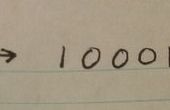Paso 10: Una fórmula para "puros" de repetición de decimales


Es decir, antes de estas fracciones reducidas, tienen un montón de nueves en ellos. La razón por qué el denominador siempre viene de la diferencia de dos potencias de 10 durante el truco de la substracción se muestra en el paso 7, por ejemplo, 10-1 = 9, 100-1 = 99, 1 1000000 = 999999, 1000-100 = 900
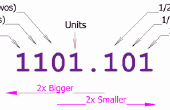
Ahora, consideremos el caso especial de los decimales de repetición, para que la parte entera es cero, y no hay ninguna parte no se repiten. Es decir la parte de repetición es empujada derecho contra el punto decimal, como los siguientes ejemplos:
¿Ves el patrón? El numerador es la secuencia de repetición. El denominador es un entero compuesto enteramente de nueves, y tiene la misma longitud que la secuencia de repetición.
Para este truco funcione, la repetida fracción tiene que ser en la forma que se muestra arriba, concretamente se tiene que tener cero parte entera, y tiene la parte repetición inmediatamente después del punto decimal. No sé si hay alguna jerga oficial matemáticas de esta forma, pero para los efectos del presente Instructivo, voy a llamar a esta forma de "puro decimal de repetición"
¿Por qué llamar puro? Yo lo llamo este decimal de repetición, «puro», porque no tiene ninguna parte entera, y no tiene parte no se repiten. La única parte que tiene, es la parte decimal de repetición.
Obviamente merece un nombre especial ya que tiene esta propiedad de ser igual a una fracción con la secuencia de repetición, como un entero, para el numerador y un denominador de la misma longitud que el numerador, componen de los nueves, es decir es (10n -1), donde n es la longitud de la secuencia.
Otra propiedad interesante de puras repetición de decimales, es son casi siempre correctas, es decir, menos de 1.
El único ejemplo de un decimal de repetición puro incorrecta es:
0. [9] es incorrecto porque no es menos de 1.
Este improperness puede conducir la manera para algunos resultados extraños. Por ejemplo la expresión:
no tiene una parte de la fracción propia. Supongamos que quiero escribir esto como una fracción mixta. Sólo he acepto que el hecho de que todas las cosas en el lado derecho del punto decimal son también igual a 1.
La segunda foto de este paso muestra una máquina expendedora de combustible con el precio, 1.999. Este número es aproximadamente igual a 2. La aproximación se convierte en exacta cuando usted tiene un número infinito de nines, como se indica en la ecuación anterior.