Decimal a fracción (11 / 12 paso)

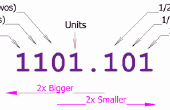
Paso 11: Usando la fórmula de «puros» de repetición de decimales

El truco aquí es ampliar el número decimal como una suma de su parte entera, la parte no se repiten, y lo que queda. La parte de lo que sea-es-sobra contendrá un decimal de repetición pura veces una potencia de 10. A continuación, utilizar la fórmula de un decimal de repetición pura para encontrar la fracción equivalente de f(p) = p / (10ⁿ-1) luego que sustituir esa fracción en la expresión anterior.

Vamos a revisar uno de los decimales de repetición del paso 7.

De inspección esto es un decimal de repetición impuro porque tiene una parte no se repiten. También tiene una parte entera, que es otra razón por qué no es puro.

Ampliar este decimal como una suma de su parte entera, la parte no se repiten, y lo que queda.

El término medio es igual a 45/100 y el último término es igual a (1/100) * 0. [6]

Utilizando la fórmula para un f(p) decimal, repetición pura = p / (10ⁿ - 1), encontrar el 0. [6] = 6/9 = 2/3. Substituir esto en la expresión anterior y obtenga:

Encontrar un denominador común para los dos términos fraccionarios y agregar juntos. Esto da una respuesta en forma de fracción mixta.

Convertir una fracción impropia, para comprobar que es el mismo resultado que uno encontró en el ejemplo en el paso 7.

Otro ejemplo:

Este decimal tiene cero entero y no es de repetición que consiste en dos ceros. La parte repetitiva no "toca" el punto decimal, así este decimal de repetición no puede ser puro.

Sin embargo es igual a (1/100) * 0. [45] y 0. [45] = 45/99 es un decimal de repetición puro.