Decimal a fracción (12 / 12 paso)

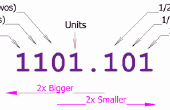
Paso 12: Todo lo demás es irracional

En los pasos anteriores he mostrado a ti, dos tipos de números decimales: el tipo que terminan en un decimal de repetición y la clase regular que sólo final, o equivalente, termina en una cadena de ceros finales. Estos dos que era capaz de convertir en una fracción, un cociente de dos enteros. Resulta que esta es la definición de los números racionales.

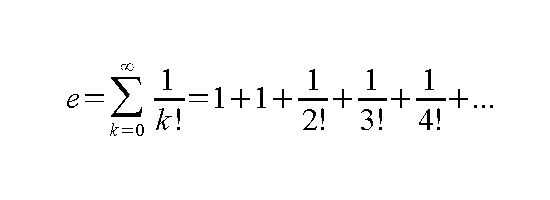
Pero hay más cosas por ahí. Hay números cuya representación decimal tiene un número infinito de dígitos, pero las cifras no se repiten. Estos números no se pueden expresar como el cociente de dos enteros, y esta es la definición de un número irracional.

Los sospechosos habituales, pi, e, 2^1/2, tiene las siguientes representaciones decimales aproximadas:

PI = 3.1415926535898...

e = 2.718281828459...

2^1/2 = 1.4142135623731...

Al final de cada una de estas aproximaciones he colocado un punto-punto-punto.

Al final de un punto-punto-punto de la secuencia decimal de repetición de un número racional, significa "etcétera", que significa más de lo mismo.

Sin embargo simplemente punto-punto-punto colocado aquí indica que continúa la secuencia, y no sé lo que va a hacer a continuación.

Tal vez se pregunte qué es lo que impulsa estos números irracionales para producir estas secuencias interminables de dígitos, y la respuesta es la misma que siempre fue: grandes cifras en números más pequeños.

Los siguientes enlaces pueden explicar esto más completamente que pueda.

http://MathWorld.Wolfram.com/RationalNumber.html
http://MathWorld.Wolfram.com/RepeatingDecimal.html
http://MathWorld.Wolfram.com/IrrationalNumber.html
http://en.wikipedia.org/wiki/Rational_Number
http://en.wikipedia.org/wiki/Irrational_number