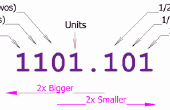
Paso 4: División de larga: la cuna de la repetición de decimales

Considerar la división larga de 20 por 9.
9 primera entra 20, 2 veces, con un resto de 2. Que 2 tiene un cero que se arrastra, por lo que el dividendo para el siguiente paso es 20.
Entonces 9 entra 20, 2 veces, con un resto de 2. Que 2 tiene un cero que se arrastra, por lo que el dividendo para el siguiente paso es 20.
Entonces 9 entra 20, 2 veces, con un resto de 2. Que 2 tiene un cero que se arrastra, por lo que el dividendo para el siguiente paso es 20.
.. .y la respuesta sigue creciendo, o por lo menos la pista de 2s a la derecha del punto decimal sigue creciendo.
A medida que agrega más 2s detrás del punto decimal la suma es más grande, pero sólo en cantidades minúsculas. En realidad la suma se aproxima a un número concreto, y que número es exactamente 20/9, y resulta que el valor exacto de 20/9 son un número que no se puede escribir en forma decimal, o al menos no sin un número infinito de 2s.
Para tomar prestada una frase del campo de la informática, el problema con los decimales de repetición es especie de un "error". Es un error inherente en el diseño de números decimales. Lo que puedo decir este fallo no puede ser "fijo". Sin embargo hay una solución.
La solución consiste en dibujar un pequeño bar en la secuencia de dígitos que se repite y luego llamar buena.
El pequeño bar significa "la secuencia de dígitos debajo de esta barra se repite para siempre". En serio. Es lo que significa.