Paso 7: Opcional: detalles del algoritmo

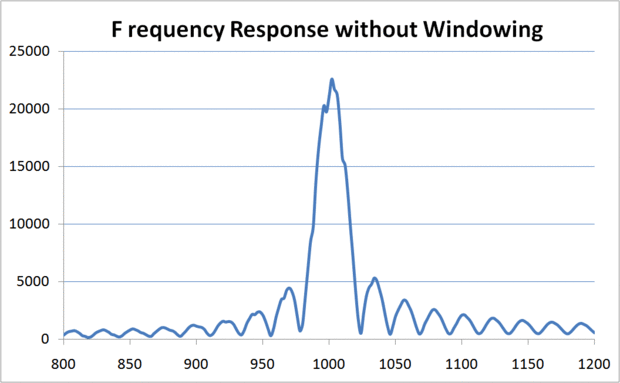
El algoritmo actúa como un filtro de paso de banda muy estrecha. Produce una respuesta muy fuerte a las frecuencias dentro de la banda de paso y una respuesta mucho más baja para las frecuencias fuera de la banda de paso. Los detalles minuciosos del algoritmo de Goertzel no cubiertos aquí.
El lazo del algoritmo muestrea la entrada usando el microprocesador construido en convertidor A/d. Se realizan las operaciones matemáticas necesarias en el tiempo entre muestras sucesivas.
Las diferentes variables utilizadas en el algoritmo se definen como sigue:
Xn_sample = la última muestra del convertidor A/D
Xn = la muestra más reciente del convertidor A/D multiplicado por la función de la ventana.
Y0 = el valor de salida se calcula en la actualidad.
Y1 = el valor de salida previamente computada. (El valor de la salida de la iteración anterior del bucle).
Y2 = el valor de salida de la iteración iteración antes de la iteración anterior l del bucle.
La figura siguiente muestra una lista de las variables utilizadas en el algoritmo.
Consulte el diagrama de flujo en el PDF adjunto para ver cómo la porción de algoritmo de Goertzel del programa se ejecuta en el procesador. Una vez que el algoritmo tiene procesos de todas las muestras (los archivos *.hex y *.asm adjuntos utilizan para 200 muestras), se calculan los componentes real e imaginarios de los resultados. Las partes real e imaginarias se utilizan para calcular la magnitud. La magnitud es que una medida de la frecuencia objetivo está presente en los datos muestreados. La magnitud se compara contra el umbral. Si el valor es mayor que el valor de umbral, la frecuencia se considera para ser detectado, y la salida se encuentra alta. Si la magnitud es inferior al umbral, la salida se encuentra baja.
La agudeza de la respuesta del filtro versus frecuencia es proporcional al número de muestras tomadas. La respuesta del algoritmo debe ser aguda que responde a la frecuencia de objetivo pero produce mucho menor respuesta para frecuencias situadas fuera de la meta. Un valor de 200 muestras fue encontrado para producir una respuesta razonablemente estrecha en experimentación.
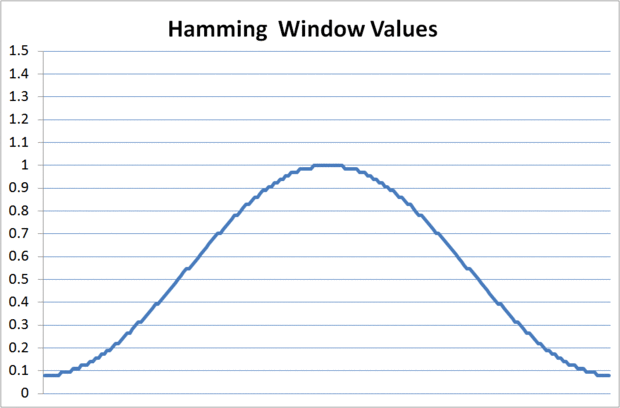
Función de visualización en distintas ventanas
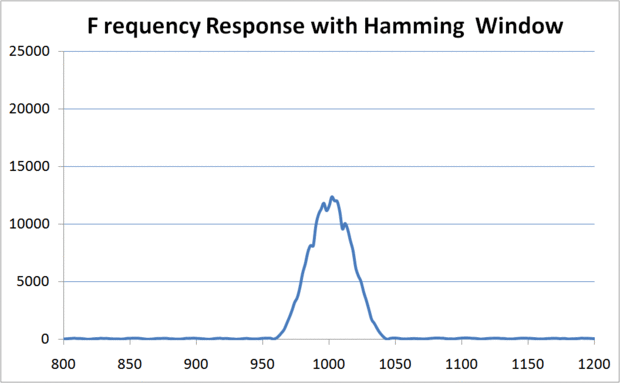
Después de cada muestra se obtiene del convertidor A/D, en primer lugar se multiplica por un valor de ventana antes de ser utilizados en los cálculos posteriores. Consulte las fotos de abajo que muestra la respuesta de frecuencia del algoritmo para ver los efectos de la ventana. La magnitud de la respuesta es menor y la anchura de la respuesta es mayor cuando se utiliza la ventana, pero ondas casi son eliminados, facilitando la determinación de si la frecuencia de la blanco está presente.
Hay muchos tipos de ventanas que se pueden aplicar en procesamiento digital de señales. Este particular se llama una ventana de Hamming. En un cuadro a continuación se muestra la forma de la ventana de hamming. El diagrama siguiente muestra el valor de la función de ventana que se utiliza para cada una de las muestras en la subrutina.