Paso 1: Matemáticas rusa Bros


Georgy Voronoy fue un matemático ruso. El diagrama que lleva su nombre se utiliza para dividir un plano llenado de nodos únicos en regiones separadas. Lo cool de estas regiones es que en cualquier punto dentro de ellos, estás más cerca de los nodos que contienen que cualquier otro nodo, y, en cualquier punto a lo largo de sus límites, es equidistantes a por lo menos dos nodos. Esto los hace muy útiles para muchas aplicaciones tales como mapeo y zonificación.
Boris Delaunay, otro Matemático ruso y estudiante de Voronoy, desarrolló un método para conectar los nodos de la misma en regiones triangulares, que es esencial en el proceso de creación de diagramas de Voronoi. Lo importante en una triangulación de Delaunay es que, en cada triángulo generado, no hay otros nodos existen en el circumcircle de ese triángulo particular. Se trata de una forma elegante de decir que cada triángulo está formado por la conexión de cada nodo a sus vecinos más cercanos.
Curiosamente, Delaunay fue también un consumado alpinista, que puede explicar por qué su método de triangulación se utiliza a menudo para construir las lata superficies al terreno del modelo en 3D. Guardaremos para otro día...
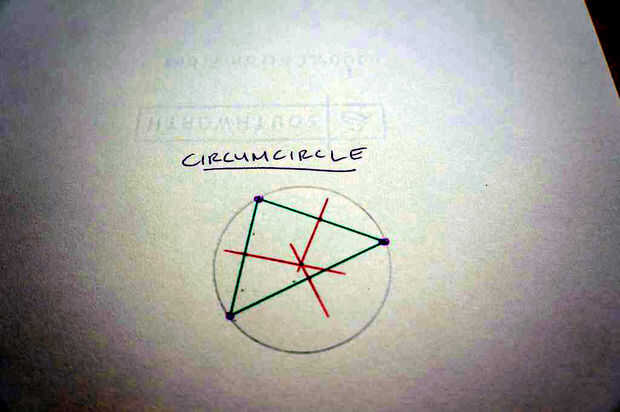
Para los que preguntan sobre eso circumcircle goofy... es un círculo que interseca cada uno de los vértices de un triángulo. Su centro se encuentra donde se cruzan los Bisectores perpendiculares de cada uno de los tres lados, y su radio es la distancia desde este punto a cualquiera de los tres vértices. Aunque no necesariamente tenemos que dibujar todos los circumcircles más adelante, los puntos de centro mencionados será muy importantes. Más como viene.
Así que, gracias a estos dos tíos frescos, podemos realizar algunos análisis bastante impresionantes y hacer algunas ilustraciones de aspecto interesante también.
Si quieres leer un poco más entonces aquí están algunos enlaces:
Triangulación de Delaunay: https://en.wikipedia.org/wiki/Delaunay_triangulat...
Patrón Voronoi: https://en.wikipedia.org/wiki/Voronoi_diagram
Boris Delaunay: https://en.wikipedia.org/wiki/Boris_Delaunay
Georgy Voronoy: https://en.wikipedia.org/wiki/Georgy_Voronoy













