Paso 9: Conversión a velocidad Angular y aceleración Angular media
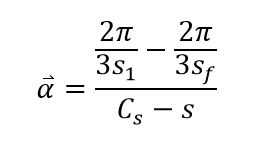
Como se mencionó, será útil para convertir los intervalos de tiempo en velocidad angular y luego media aceleración angular. Nota que la velocidad está dada por Δθ/Δt y esa aceleración angular viene dada por (Δθ/Δt) / Δt. Puesto que cada impulso representa el tiempo necesario para que la rueda gire 2π/3 radianes, el promedio de la velocidad angular, ω, es igual a 2π/3s, donde s es el intervalo de tiempo en milisegundos. Para calcular el promedio aceleración angular, α, (desaceleración en este caso), tenemos que pensar en los puntos primero y último. Por lo tanto, α = ((ω_f) - (ω_1)) / T, donde T = C - s o el total menos el primer impulso y ω_f es la velocidad angular final y ω_1 es la velocidad angular inicial (esta fórmula es en la foto superior). El resultado final debe ser multiplicado por 100000 para producir una respuesta en segundos en lugar de milisegundos. Esta fórmula puede aplicarse a cada celda de que la misma manera los datos se filtró por la instrucción if-then. Para la primera columna de un determinado conjunto de datos en excel, esto es lo que quisiera incluir en la barra de fórmulas:
=(((2000*PI())/(3*A84))-((2000*PI())/(3*A1)))/((SUM(A1:A84)*0.001)-A1*0.001)
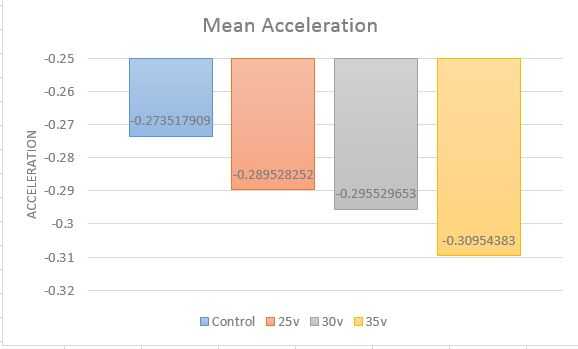
Esto entonces se puede aplicar a todas las otras columnas (nota que A84 es la última celda de datos en mi caso, pero variará de conjunto de datos al conjunto de datos y una voluntad de cambiar dependiendo de la columna). Una vez que se calcula la aceleración angular promedio para cada conjunto de datos, los quince valores resultantes pueden ser promediados para obtener un valor único, con todo incluido para ese nivel específico. Estos valores se pueden graficar como un gráfico de barras similar a la que se incluye. Tenga en cuenta la tendencia en las alturas de las barras. Esto sugiere que existe una relación directa entre la tensión suministrada al solenoide y el correspondiente frenado fuerza; sin embargo, no hay pruebas suficientes para establecer conclusiones con respecto a la significación estadística. Estadística inferencial es útil en este momento con el fin de permitirnos hacer las conclusiones deseadas.