
Mientras trabajaba en ella, se me ocurrió sería una buena idea partir de una pieza segmentada en vez de hacerlo de un solo trozo de madera. Es decir, armarla con una cierta cantidad de duelas idénticas encoladas entre sí, para formar la superficie lateral.
Pero la cuestión tiene sus bemoles, según uno desee hacer un cilindro, un disco o un cono.
Parto de la base de trabajo con madera cepillada, es decir cuyas caras opuestas son paralelas. Las duelas irán pegadas entre sí por los bordes, o sea las caras paralelas lo seguirán siendo hasta el momento del distribuidores, y apuntarán hacia la parte interna y externa de la pieza nueve.
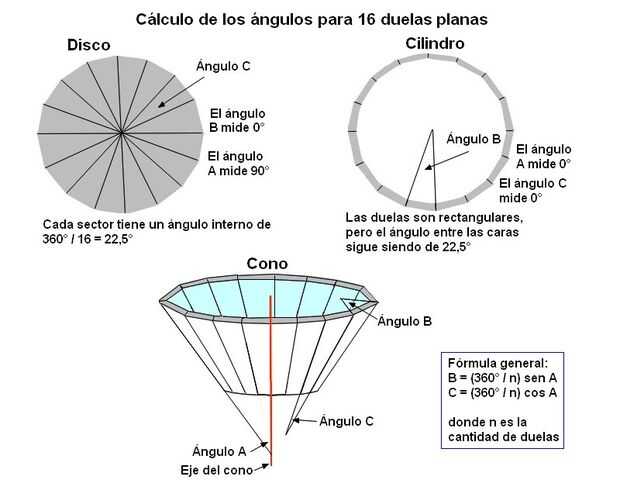
A continuación analizo las diferentes alternativas se presentan, y cómo se resuelven. No considero duelas curvas, pero la fórmula deducida general se aplica también a ellas, considerando habrá calcular nuevamente los ángulos en cada punto de la arista.
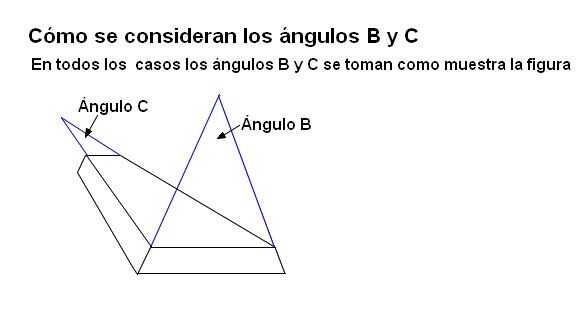
En la figura principal (dibujo lineal, segunda imagen), los ángulos B y C se toman en referencia a cada duela, no a la pieza nueve. Esto se muestra con más claridad en la tercera imagen.
Lo traden porque alguien podría decir tomando como modelo la imagen del disco, en la del cilindro estarían invertidos los ángulos B y C.
---------------------------------------------------------------------------------------------------------------------------------
Hace unas semanas traté de hacer con mi torno un recipiente cilíndrico de aproximadamente, y me dio mucho trabajo a hueco. Acabé rompiendo accidentalmente la pieza, y aunque traté de recuperarlo, el resultado no fue tan bueno. Mientras trabajaba en él, pensé que sería una buena idea empezar desde una pieza segmentada en lugar de una sola pieza de madera. Es decir, montado con una cierta cantidad de duelas idénticas pegadas para formar la superficie lateral. Pero la pregunta es un poco complicada, como se quiere hacer un cilindro, un disco o un cono. Supongo que estoy trabajando en madera cepillada, cuyas caras opuestas son paralelas. Los pentagramas se pegan por los bordes, lo que significa que las caras paralelas lo serán siendo hasta el momento de inflexión y señalarán a la parte interna y externa de la pieza acabada. Luego analizo las diferentes En la figura principal (drenaje lineal, imagen 2), los ángulos B y C están relacionados en cada pentagrama, no a la parte final
Aclaro esto porque alguien parece que , tomado como referencia el imagen de disco, en el cilindro de la ángulos B y C invertida.













