Paso 5: 2 º Programa de procesamiento de

¿Recuerda matemáticas vectoriales 3D todo lo que de escuela que pensaste que nunca utilizaría? Vamos a lo todavía no tienen que usarla ya que he hecho para usted.
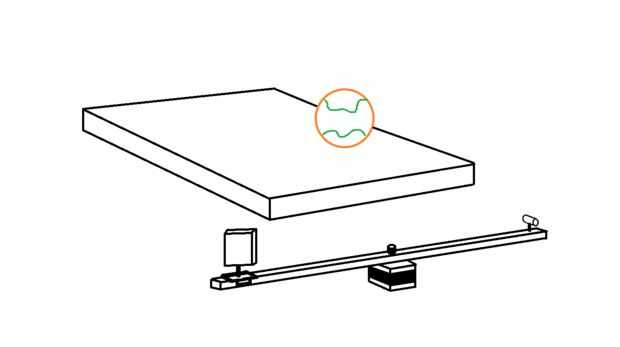
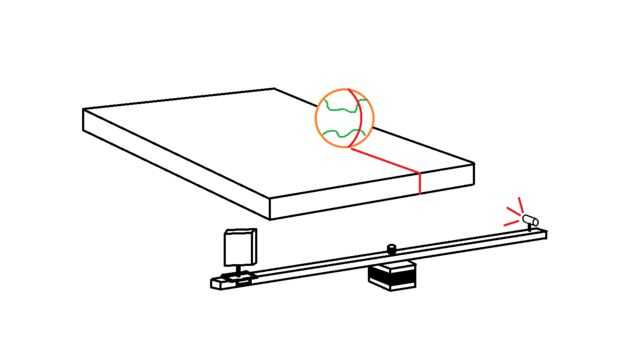
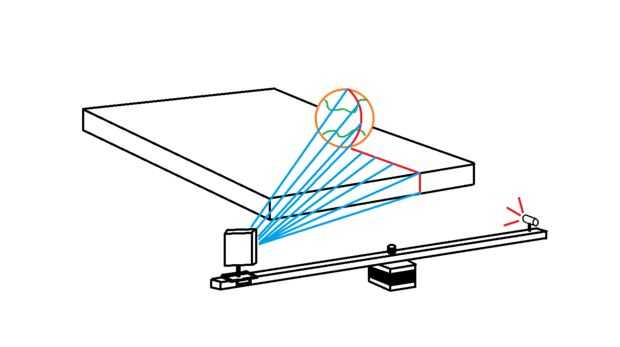
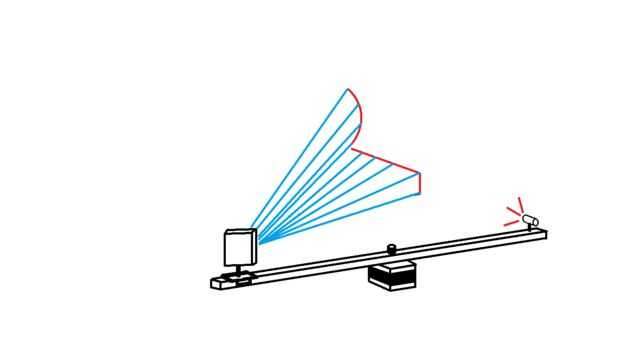
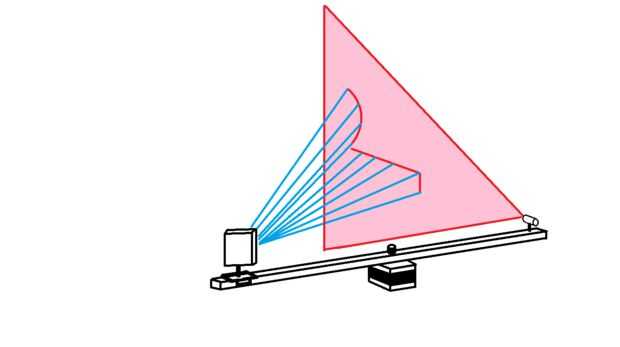
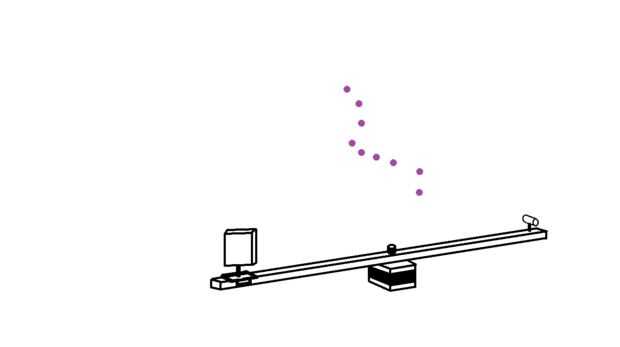
En esta parte final se escriba otro sketch de procesamiento que lleva las coordonadas de píxel blanco y proyectos que sobre el plano creados por el láser lineal. Cada pixel blanco se convierte en una línea imaginaria que sale de la cámara en el espacio 3D. Donde cada línea interseca con el plano de láser imaginario, un punto de datos se trazarán. Esto se repite para cada pixel blanco en cada fotograma de la webcam, eventualmente construir una nube de puntos 3D. Solo ver el video...
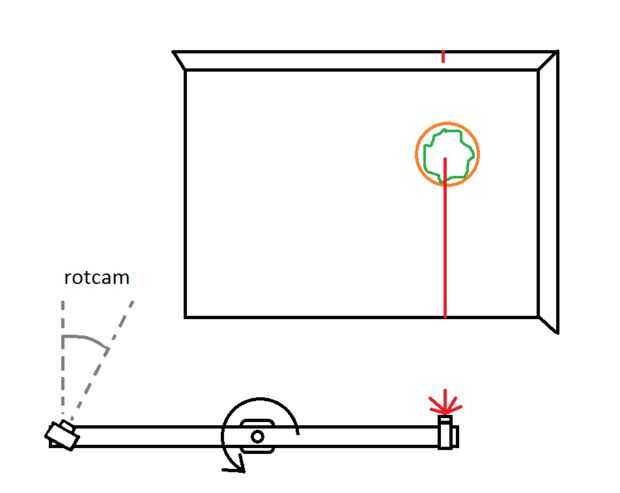
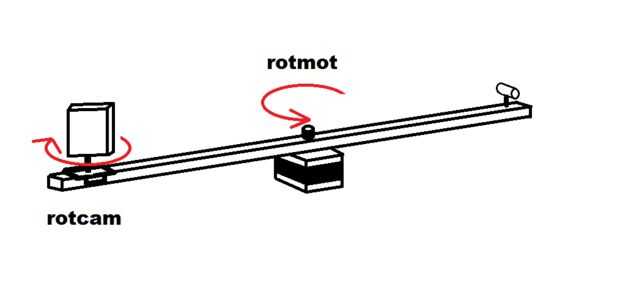
La única parte de la configuración que mencionaré aquí es el parámetro 'rotcam'. Esto es donde usted necesita introducir el ángulo de la cámara, donde 0deg es mirando recto hacia adelante, y 90deg está mirando el laser. Debe quedar entre 10 y 40 grados dependiendo de lo que estamos digitalizando. Pequeños ángulos de lejos objetos y ángulos más grandes para cerrar los.
Para comenzar con en el circuito de drenaje que tenemos que ampliar los planos de recorte usando 'perspectiva' esto es parada muy lejos y lo cerca de desaparecer. Entonces tenemos que crear 3 líneas para representar la X, Y y z y hacerlos rojo, verde y azul.
A continuación podemos configurar nuestra cámara que utilizamos para mirar el espacio 3D. Podemos utilizar pecado y lechuga romana junto con la posición X del ratón en la pantalla para crear un efecto de plato para ver al tema más fácilmente. Jueguen con esto por consiguiente para obtener algo cómodo de usar.
Así que ahora estamos saltando en el bucle que hace la matemáticas. Sin embargo sólo queremos que se ejecute si se presiona cualquier tecla. Esto significa que sólo debe hacer los cálculos una vez en lugar de repetir una y otra vez.
Aquí tenemos que cargar el archivo de texto con las coordenadas del pixel blanco y guardarlo en un vector de string 'miCadena'. Honestamente, no sé por qué tiene que ser un vector, solo toma el primer elemento pero se niega a trabajar si es sólo una cadena. BIEN entonces tenemos que vectores de gran flotador vacío X, Y y Z de coordenadas donde cada uno se llenará con el componente XYZ correspondiente de cada solo punto de datos en la nube de puntos.
'miCadena 'deben dividirse cada fotograma de webcam usando splitTokens para';'. Esto tiene re-escrito 'miCadena' como un vector con las coordenadas de un fotograma de la cámara en cada elemento.
Ahora podemos saltar en un bucle que se repite una vez para cada marco de cámara guardado en miCadena.
A continuación necesitamos hacer otro vector de cadena llamada 'stringPart' que divide aún más 'miCadena'. Divide en individual X y Y blanco coordonadas de píxel ahora contenidas en cada elemento. Esto es sólo guarda un fotograma a la vez.
Ángulo actual del motor se guarda en 'rotmot' y viene del primer elemento de la 'stringPart', vector se convierte en un flotador.
Este siguiente poco, nuestro espacio 3D a partir de punto (0,0,0) es el centro del eje del motor en la superficie del brazo.
Aquí utilizamos una función llamada pushMatrix. Esto se utiliza para cambiar nuestra posición en el espacio 3D local, básicamente cambia Dónde está el centro de nuestro universo 3D. Entonces podemos usar las funciones de modelX, Y, Z para encontrar el verdadero mundiales coordenadas de un punto después de pushMatrix traducciones y rotaciones. Cosas muy utiles! Así que dentro de este primer pushMatrix, gire en Y por el ángulo actual de motores.
Luego ir a otro pushMatrix (una dentro de otra) y traducir desde centro del eje del motor a lo largo del brazo al láser. Aquí podemos crear la ecuación para el plano láser lineal. Cuando digo plano láser, estoy hablando sobre un plano donde el láser puede brillar en cualquier punto a lo largo del plano. Así que el avión va a través del laser y nada brilla en.
Para que la ecuación del plano, necesitamos dos puntos que hacen una línea perpendicular al plano láser. Se trata NORMAL VECTOR del plano. La ecuación se deriva de esto y un punto en el plano.
Luego usamos popMatrix para deshacer lo que hizo el pushMatrix. Solo la usamos una vez para volver al centro de motores pero con su transformación de rotación.
En esta siguiente parte, trabajamos dentro de otro bucle que funciona una vez para cada píxel blanco, así que sea la longitud del stringPart pero incrementa en dos. Esto es porque queremos usar coordenadas X y Y en este bucle al mismo tiempo.
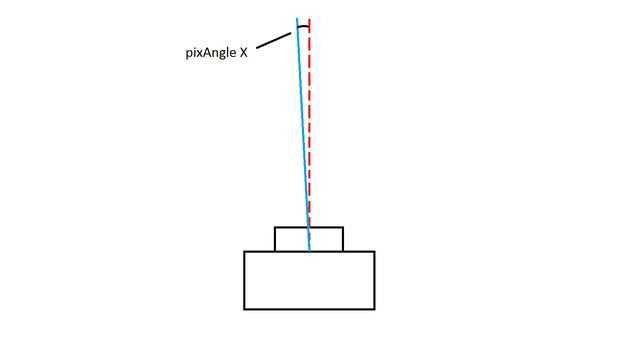
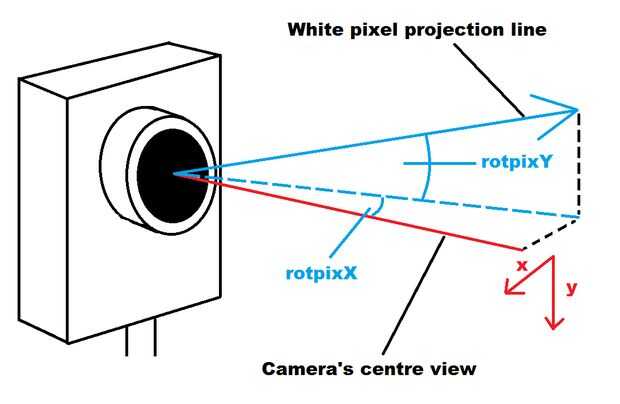
Así que ahora estamos trabajando con un único píxel blanco que se convertirá en un solo punto de datos. En este bucle primero tenemos que convertir las coordenadas XY de píxeles blancos en ángulos que actúan como el XY los ángulos de la línea de proyección imaginaria desde el centro de la visión... cheque las imágenes para ver lo que estoy hablando.
Ahora tenemos que volver a utilizar pushMatrix y movimiento del eje del motor a lo largo del brazo hasta el centro de las cámaras. Gire en Y por el ángulo de la cámara y finalmente nos gire en X y Y con los ángulos se describe en el último párrafo. Ahora nuestras coordenadas locales están en la cámara, apuntando directamente hacia afuera a lo largo de la línea de proyección de un único píxel blanco.
Ahora hacemos la línea de proyección de la misma manera que hicimos el vector normal del plano. Hacer un punto en el centro de la cámara y otro punto a cierta distancia a lo largo de la línea de proyección. De esto podemos hacer la ecuación para la línea.
Aquí nos aparecerá la matriz para volver al eje del motor con la rotación del motor.
Ahora utilizamos una versión cambiada de la ecuación del plano con la ecuación de la línea insertada en él y resolver para ' t '. Ver la ecuación reorganizada en las imágenes. Entonces el resultado de la materia para ' t ' en las ecuaciones de la línea XY y Z. Así que ahora tenemos nuestras coordenadas XYZ para un solo punto de datos. Empujar en los vectores 'drawpoint' que llevan a cabo cada punto.
Utilizar popMatrix de nuevo para volver a los inicios del sistema global de coordenadas sin traducciones o transformaciones de rotación.
Así que ahora tenemos 3 grandes vectores para XY y Z componentes de todos los datos del punto pero realmente no han dibujado los puntos de la nube de puntos. Así que podemos hacer ahora. Usar un bucle recorrer cada punto de datos lo que como mucho tiempo como 'drawpointX' y en el bucle, use ' point(drawpointX[i],drawpointY[i],drawpointZ[i]). Esto traza un punto en cada intersección entre la línea de proyección de un píxel blanco y el plano láser.
Eso es todo, bien hecho! Golpe solo ejecutar y pulse cualquier tecla para renderizar la escena. Asegúrese de que el archivo que intenta leer de se guarda en la carpeta de este sketch.













