Paso 3: Teoría común tijera
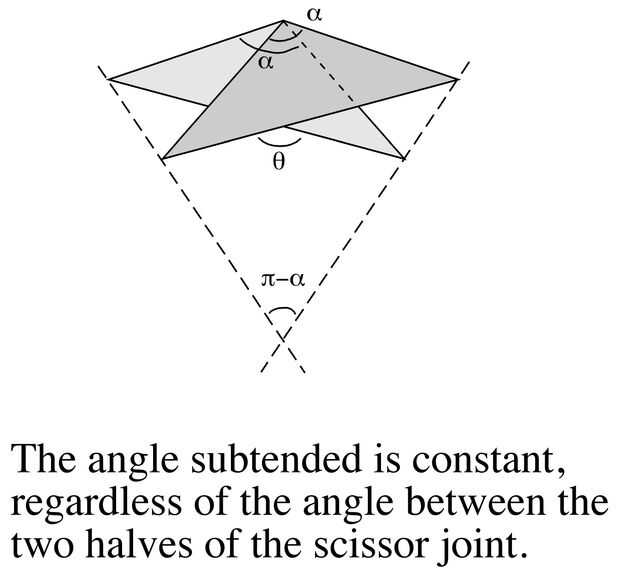






Esta figura muestra el teorema matemático detrás de la operación de este modelo. Establece que si dos triángulos están conectados juntos en un pivote como se muestra, la línea punteada que conecta los vértices (el plural de vértice--matemáticas habla de «el rincón») se cruzan en un ángulo constante, independientemente de cómo los triángulos se rotan. La prueba se deja como ejercicio para el lector.
Porque nuestros triángulos (que en realidad son la mitad de los rombos) tienen un ángulo obtuso de 135 grados, el ángulo entre la línea punteada es 45 grados. Así que 8 de estas juntas de tijera se pueden vincular en un anillo (8 x 45 = 360) y deslice hacia adentro y hacia afuera suavemente. Tres de estos anillos se pueden hacer que se entrecruzan en ángulo recto en los planos xy, yz y zx y listo--un expanden y contraen esfera!
Estas fotos muestran pares de articulaciones tijera doblar a través de su rango completo de movimiento. Cool, ¿EH?













