Paso 5: Calcular el índice de refracción de gelatina
![]()
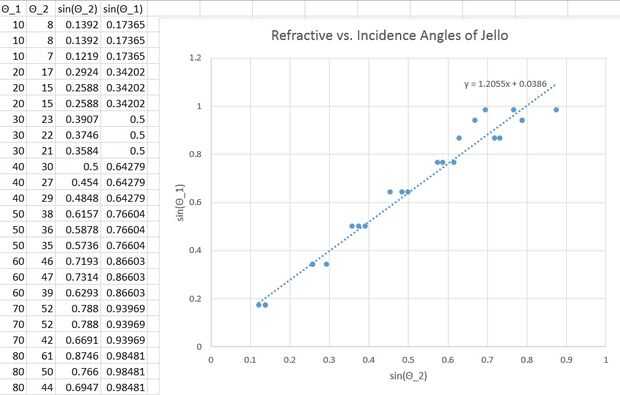
Ley de Snell se utilizará para determinar el índice de refracción. Ley de Snell da una relación entre el ángulo de la incidencia Θ_1 y su medio n_1 de índice de refracción y el ángulo de refracción Θ_2 e índice de refracción n_2 de su medio usando la ecuación n_1*sin(Θ_1) = n_2 * sin(Θ_2). El medio que se recorre el ángulo de incidencia en este caso es simplemente aire, cuyo índice de refracción se sabe que aproximadamente 1, y así podemos simplificar la ecuación anterior y solucionar para el índice de refracción de la gelatina: n_2 = sin(Θ_1)/sin(Θ_2). Promedio del ángulo de refracción en cada grado medido y crear un gráfico de los senos de los ángulos de refracción vs los senos de los ángulos de incidencia (valores de la X son los ángulos de refracción, y los valores de Y son los ángulos de incidencia). Crear una línea de mejor ajuste de los datos. El índice de refracción de gelatina será la pendiente de esta línea.
Nuestro gráfico (mostrado arriba) tenía un mejor ajuste de línea con una pendiente de 1.21, que nos dijo que nuestro experimento admite el índice de refracción de gelatina es 1.21.
Al finalizar esta experiencia, aprendimos muchas cosas. Nos dimos cuenta de que puede ser difícil ver la luz refractada de un láser rojo en gelatina cereza. Esta dificultad podría han dado lugar a errores de medición de ángulo de refracción, que conducirán a un índice de refracción incorrecta. Experimentos en el futuro que le recomendamos usar un color más claro. Sin embargo, creemos que esto es una experiencia beneficiosa para el aprendizaje porque este método puede utilizarse para encontrar el índice de refracción de los materiales más transparentes, que será de utilidad para cualquier estudiante de óptica.