Impresión Quasicrystal formas 3D (1 / 5 paso)

Paso 1: Generación de quasicrystals de onda plano

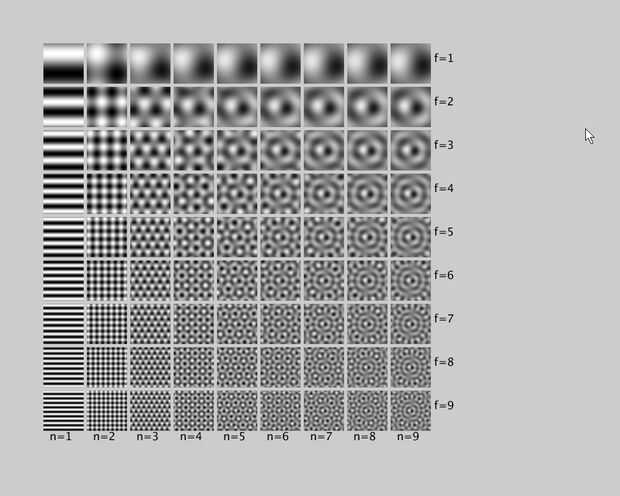
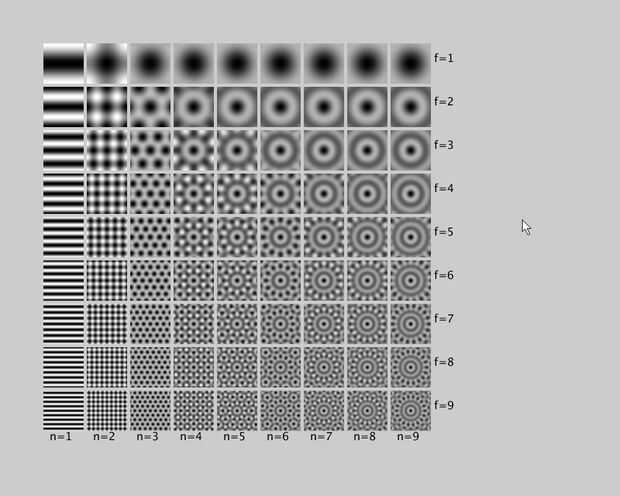
Si bien hay una gran variedad de quasicrystals incluyendo embaldosados de Penrose y los patrones de difracción de rayos x, los que estoy usando aquí se generan mediante la suma de ondas planas. Imagine una onda sinusoidal plano: se ve como cartón corrugado pero se extiende hasta el infinito. Si pones algunos de éstos junto con las ondas en diferentes ángulos y suma todo, se obtiene un quasicrystal. Aquí es un blog que ilustra la idea. Para ver las clases de patrones que se pueden generar, he creado algunos patrones de prueba con diferentes números de ondas planas en diferentes frecuencias. Aquí, n es el número de ondas de diferentes planas,: la fila izquierda es n = 1 donde hay solamente una sinusoide que no es muy interesante. "f" es la frecuencia o el número de ondas que caben en la Plaza. La fila superior muestra f = 1 donde sólo un ciclo de ajustes en el cuadro. Cuando proceda hacia abajo, es como el zoom como ciclos cada vez más visibles.

Las dos imágenes muestran las ondas sinusoidales (en la parte superior) y las ondas del coseno (en la parte inferior). Cero está en el centro de la imagen, y ondas planas son centradas en gira alrededor de él. Tenga en cuenta que desde pecado (x) = - x los patrones sinusoidales son antisimétrico: la mitad izquierda es el inverso de la mitad derecha. Ondas del coseno, por el contrario son simétricas: cos (x) = x por lo que los patrones del coseno en la parte inferior son perfectamente radialmente simétricos.