Paso 8: matemáticas!!!!!!
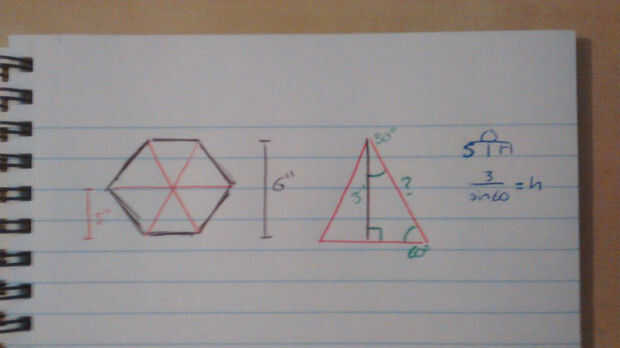
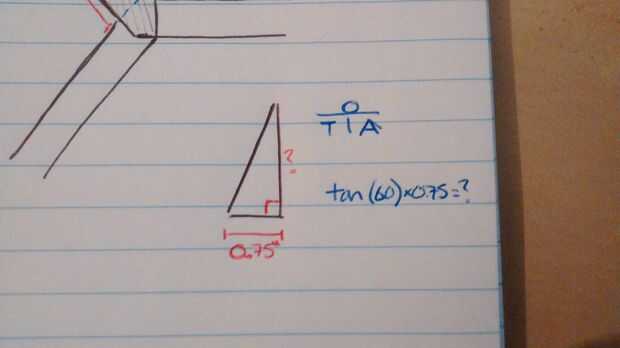
Como prometido, algunas matemáticas aquí para que usted pueda trabajar hacia fuera Qué tamaños que usted necesite para diferentes tamaños de ollas. Tendrás que aguantar fotos de garabatos, porque MS paint es más difícil que una pluma y mi teléfono. Aunque mi teléfono luchan por foco sin luz natural.
Un hexágono para sostener una olla de 6" debe ser 6" en la dimensión interna más pequeña (de lado a lado), y necesitamos saber la longitud de un lado. Un hexágono puede ser considerado como 6 triángulos equiláteros. Si el conjunto es de 6" a través, cada triángulo es 3" alta (lápiz rojo). Si se corta ese triángulo por la mitad, tiene un triángulo de ángulo recto de 3" por un lado (lápiz verde).
Ahora necesitamos saber la longitud de la hipotenusa (el borde inclinado). Trigonometria puede decir que esto es dividido por el pecado (60 grados) (el ángulo enfrente del lado utilizamos la longitud de) de 3". Esto resulta ser ~ 3,5"(3.464101615...)
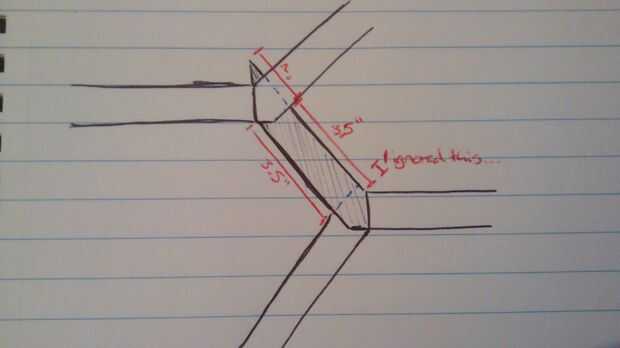
Si está montado como el mío, también hay que 3.5" entre donde se cruzan los lados unos sobre otros y donde se encuentran los montantes. Esto es un poco más doloroso para hacer ejercicio. Tratan esta mintiéndome a mí mismo y diciendo que sólo necesitaba 3.5" además de las secciones de ángulo en cada extremo, y ajustando el corte a lo que hizo trabajar (esto también contribuyó a la deformación en mi jardinera). También necesitará usar trigonometría aquí. Tan(60) x espesor madera (0,75" para mi) le dará la longitud de la sección inclinada de la pieza (1,299"). Doble y añadir a la anchura de la hexagonal elaborado por encima de. (3.5 + 1.3 + 1.3 = 6.1)
Realmente espero que este paso ayudado alguien, porque es realmente difícil de escribir. Y todavía no creo que hice un buen trabajo.













