Paso 7: La simplificación (optimización) el camino
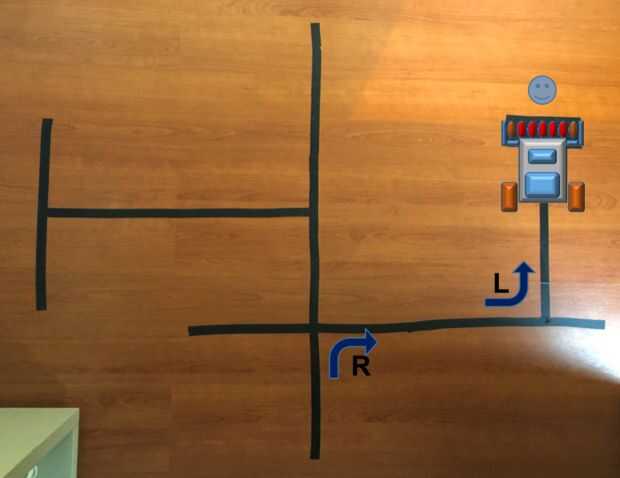
Volvamos a nuestro ejemplo. Mirando el primer grupo de intersecciones, nos dimos cuenta de la la primera rama izquierda es en realidad un "callejón sin salida" y por lo tanto, si el Robot en lugar de una "izquierda izquierda atrás" sólo pasa directamente a ese primer cruce, un montón de tiempo y energía se ahorraría! En otras palabras, una secuencia "LBL" en realidad sería el mismo que "S". Eso es exactamente cómo puede optimizarse la ruta completa. Si analizarla usted todas las posibilidades donde se utiliza un "U turn", el conjunto de 3 intersecciones donde este "giro de 180 grados" ("B") aparece ("xBx") pueden ser reducida a sólo uno.
Lo anterior es sólo un ejemplo, a continuación encontrará la lista completa de posibilidades (probarlo):
- LBR = B
- LIBRAS = R
- RBL = B
- SBL = R
- SBS = B
- LBL = S
Tomando la ruta de acceso completa o nuestro ejemplo, nosotros podemos reducirlo:
path = [LBLLLBSBLLBSLL] == > LBL = S
path = [SLlibrasBLLBSLL] == > libras = R
path = [SLRBLLBSLL] == > RBL = B
path = [SLBLBSLL] == > LBL = S
path = [SSBSLL] == > SBS = B
path = [SBLL] == > SBL = R
path = [RL]
¡ Increíble! Mirando el ejemplo es muy claro que si el robot tiene derecho en el primer cruce y luego a la izquierda, llegará el final del laberinto en la ruta más corta!
El primer camino de laberinto Solver código total se consolidará en la función mazeSolve(). Esta función es de hecho la función loop() usado antes, pero incorporando todos esos pasos de optimización almacena y camino.
Cuando terminó el primer sendero, la matriz [] de camino tendrá la ruta optimizada. Se introduce una nueva variable
unsigned int estado = 0; Resolución = 0; final del laberinto = 1
La función de la primera ruta a continuación:
void mazeSolve(void)
{
mientras (! estado)
{
readLFSsensors();
interruptor (modo)
{
caso NO_LINE:
motorStop();
goAndTurn (a la izquierda, 180);
recIntersection('B');
rotura;
caso CONT_LINE:
runExtraInch();
readLFSsensors();
Si (modo! = CONT_LINE) {goAndTurn (a la izquierda, 90); recIntersection('L');}
mazeEnd() otra cosa;
rotura;
caso RIGHT_TURN:
runExtraInch();
readLFSsensors();
Si (modo == NO_LINE) {goAndTurn (derecho, 90); recIntersection('R');}
otra cosa recIntersection('S');
rotura;
caso LEFT_TURN:
goAndTurn (a la izquierda, 90);
recIntersection('L');
rotura;
caso FOLLOWING_LINE:
followingLine();
rotura;
}
}
}
Aquí se introdujo una nueva función: recIntersection (dirección)
Esta función se utilizará para el almacén de la esquina y también para llamar a otra función simplifyPath(), que se reduce el grupo de 3 intersecciones que implican un giro en "u" como vimos antes.
void recIntersection(char direction)
{
camino [longitud] = dirección; Almacenar la intersección en la variable path.
Longitud ++;
simplifyPath(); Simplificar el camino aprendido.
}
El crédito de la simplifyPath () función es Patrick McCabe para la ruta de código de problemas (para más detalles, visite por favor https://patrickmccabemakes.com! La estrategia de simplificación de la ruta de acceso es que cada vez que encontramos una secuencia xBx, nosotros podemos simplificar cortando el callejón sin salida. Por ejemplo, LBL == > S como vimos en el ejemplo.
void simplifyPath()
{
Si (longitud < 3 || camino [longitud-2]! = 'B') volver; sólo simplificar el camino si la segunda a la última vuelta fue una 'B'
int totalAngle = 0;
int i;
para (i = 1; i < = 3; i ++)
{
Switch(path[pathLength-i])
{
caso 'R':
totalAngle += 90;
rotura;
caso 'L':
totalAngle += 270;
rotura;
caso 'B':
totalAngle += 180;
rotura;
}
}
totalAngle = totalAngle % 360; Obtener el ángulo como un número entre 0 y 360 grados.
Switch(totalAngle) / / reemplazar todos los giros con una sola.
{
caso 0:
camino [longitud - 3] = de ';
rotura;
caso 90:
camino [longitud - 3] = 'R';
rotura;
caso 180:
camino [longitud - 3] = 'B';
rotura;
caso de 270:
camino [longitud - 3] = 'L';
rotura;
}
Longitud-= 2; La ruta es ahora dos pasos más cortos.
}