Paso 5: Teoría: generalización del concepto de



¿Cómo estos ángulos se pueden variar para producir cualquier polígono?
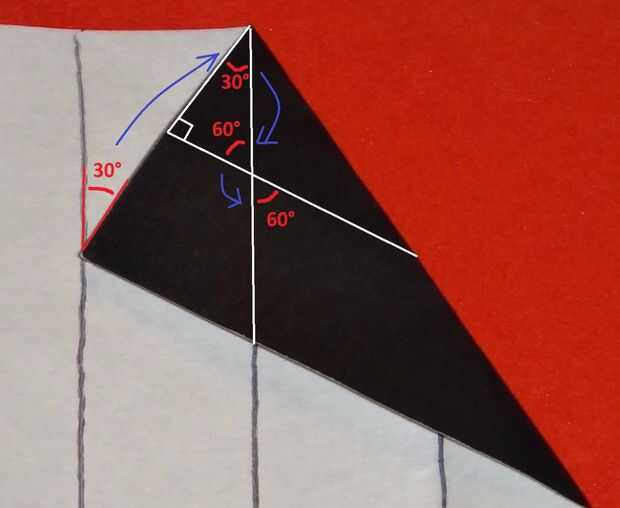
Analizar cómo se produjo el ángulo 60° interno permite el plegamiento de cualquier ángulo hasta unos 140 ° antes las unidades dejen trabar juntos. El pliegue inverso para el bolsillo utiliza los puntos de referencia de la línea central y la línea de cuarto de la izquierda. Estas líneas de referencia se utilizan para plegar un triángulo con base 1 e hipotenusa 2 de.
Θ = sine^-1(1/2) = 30°
Esto se muestra en la primera imagen.
A continuación, siga mis flechas azules de proceso de pensamiento. El ángulo de 30° puede ser prorrogado geométricamente al ángulo entre la línea central y el borde de la aleta. Ya que es un ángulo en un triángulo rectángulo, podemos encontrar el ángulo justo hacia la derecha de esto porque sabemos que dos de los tres ángulos, así como la suma de los ángulos:
180 ° - 90°-30° = 60 °
Esto puede ser llevado el ángulo entre la línea central y el doblez inverso, que forma la parte inferior de la bolsa.
En la tercera foto, tengo las dos unidades, montamos hojeadas por encima del paso anterior, que el bolsillo está todavía en el lado derecho de la unidad. Se observa que el borde derecho de la unidad se encuentra a lo largo de la reverse-fold en el bolsillo de la unidad de la izquierda. Por lo tanto, el ángulo rojo, que ya encontramos, puede ser llevado el ángulo entre las unidades. Por lo tanto, las unidades tienen un ángulo de 60°, o el interior ángulo de esquina de un triángulo equilátero, entre ellos.
Similar razonamiento, hecho al revés, puede utilizarse para encontrar pliegues de referencia suficientemente precisa para los otros ángulos, como se desee. Entender que es el ángulo de bolsillo que determina que el ángulo entre las unidades es necesario para doblar las unidades que son el borde común entre dos polígonos de diferente formados, como existen, por ejemplo, en los sólidos de Arquímedes. Un poco de trigonometría, manipulación geométrica, en algún lugar para escribir, y práctica te permite generar fácilmente una variedad de polígonos, regulares e irregulares, para hacer poliedros de.
Al hacer compuestos de poliedros, precisa unidades son importantes para hacer el modelo final encaja perfectamente. Al calcular las dimensiones del rectángulo de papel necesaria para producir una determinada longitud de borde, tenga en cuenta el siguiente artefacto del mecanismo de bloqueo. Cualquier papel pasado donde el doblez angular cruza la línea de centro (como se muestra en la última foto) no contribuirá a la longitud del borde (esto es intuitivamente obvio después de hacer algunas plegables). Por lo tanto, para las longitudes del borde de precisión, es necesario encontrar la cantidad se truncará en los extremos de las unidades y añadirlo a sus dimensiones originales de papel.