Paso 7: Control de dirección (Control proporcional - P)
Perfecto! En este punto, nuestro Robot está montado y operativo. Debe realizar algunas pruebas básicas con los motores, lea la salida de sensores y pruebas sobre una línea. Lo que falta es el verdadero "cerebro", los primeros pasos de una "inteligencia artificial". Llegaremos a esto, aplicar una lógica de control que garantice que se mantendrá el Robot siguiendo la línea.
Simple Control proporcional:
Supongamos que el Robot está funcionando sobre una línea y la salida del Sensor de matriz es: "0 0 1 0 0". El error correspondiente es "0". en esta situación, ambos motores va a correr hacia adelante en una velocidad constante:
Por ejemplo, con iniMotorSpeed = 250; significa que Servo de la izquierda van a recibir pulsos de 1, 250us y derecho Servo 1, 750us y el Robot avanzará en la mitad de velocidad. Recuerde que la velocidad de avance de Servo derecho varían con la longitud del pulso de 1, 500us (detenido) a 2, 000us (full velocidad) y la izquierda del 1, 500us (detenido) a 1, 000us (full velocidad).
rightServo.writeMicroseconds(1500 + iniMotorPower);
leftServo.writeMicroseconds (1500 - iniMotorPower);
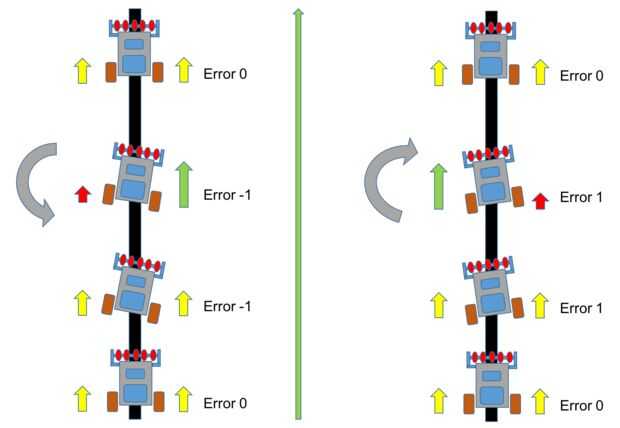
Supongamos ahora que el Robot a la izquierda (es como "la línea va a derecha") y cubrió también el sensor 3. La salida de la matriz será: "0 0 1 1 0" y el error = 1. En esta situación lo que necesita es activar el Robot a la derecha. Para ello, usted debe disminuir la velocidad del Servo de la derecha lo que significa disminuir la longitud del pulso". También, debe aumentar la velocidad del Servo de la izquierda, lo que significa disminuir la longitud del pulso del servo izquierdo. Para ello, tenemos que cambiar la función de control del motor:
rightServo.writeMicroseconds (1500 + iniMotorPower - error); == > Error positivo: disminuir velocidad
leftServo.writeMicroseconds (1500 - iniMotorPower - error); == > Error positivo: aumentar la velocidad
La lógica anterior es correcta, pero es fácil comprender que sumar o restar "1" microsegundo en longitud del pulso no generará la corrección necesaria en un tiempo realista. Es intuitivo que el número que se agrega o resta debe ser mayor. por ejemplo 50, 100, etc. Para conseguir, el "error" debe ser multiplicado por una constante "K". Una vez que la influencia de esta constante será proporcional al error, la nombramos "constante proporcional: Kp).
La motricidad será:
int Kp = 50;
rightServo.writeMicroseconds (1500 + iniMotorPower - Kp * error);
leftServo.writeMicroseconds (1500 - iniMotorPower - Kp * error);
Podemos volver a lo que sucederá con los motores como se muestra a continuación:
- Sensor de matriz: 0 0 1 0 0 == > error = 0 == > longitud del pulso del Servo derecho = 1, 750us == > longitud del pulso del Servo de la izquierda = 1, 250us (ambos motores a la misma velocidad)
- Sensor de matriz: 0 0 1 1 0 == > error = 1 == > longitud del pulso del Servo derecho = 1, 700us (más lento) == > longitud del pulso del Servo de la izquierda = 1, 200us (más rápido)
Si la situación es lo contrario y el Robot a la derecha, el error sería "negativo" y la velocidad de los servos debe cambiar:
- Sensor de matriz: 0 0 1 0 0 == > error = 0 == > longitud del pulso del Servo derecho = 1, 750us == > longitud del pulso del Servo de la izquierda = 1, 250us (ambos motores a la misma velocidad)
- Sensor de matriz: 0 1 1 0 0 == > error = -1 == > longitud del pulso del Servo derecho = 1, 800us (más rápido) == > longitud del pulso del Servo de la izquierda = 1, 300us (más lento)
En este punto es evidente que tanto el Robot a un lado, mayor será el error y más rápido debe volver al centro. La velocidad con el Robot reacciona al error será proporcional a ella.












