Paso 8: Control del PID (opcional)
En caso de saltar esta parte, está bien. Usted puede quedarse con el control proporcional, explicó en el último paso, o quemar algunos cerebros para implementar un sistema de Control más complejo en su Robot, es su opción. Vamos.
PID (proporcional, integral y derivado) es uno de los esquemas de control más comunes alrededor. Lazos de control industriales utilizan algunos sabor de control PID. Hay muchas maneras de afinar un lazo de PID, incluyendo la técnica manual utilizada en este ejemplo.
Pensar PID como un resorte simple. Un resorte tiene una longitud del original, que cuando perturbado, por expansión o contracción, tiende a recuperar su longitud original en el menor tiempo posible. Del mismo modo, un algoritmo PID en un sistema tiene un fijar-valor de una magnitud física particular para controlarse, llama un 'set point', que cuando alterado por alguna razón, el sistema de controles de las otras características necesarias en él, para volver al punto original del sistema en el menor tiempo posible. Controladores PID se utilizan cuando es necesario para controlar una cantidad física y hacerla igual a un valor especificado. Ejemplo, control de crucero en coches, Robots, reguladores de temperatura, reguladores de voltaje, etc..
¿Cómo funciona el PID?
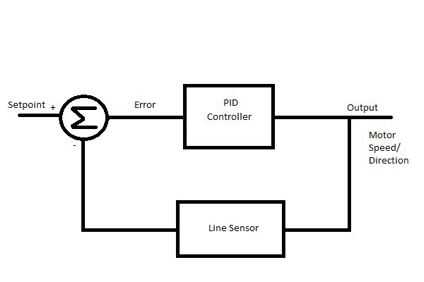
El sistema calcula el 'error' o 'desviación' de la cantidad física desde el punto de ajuste, el valor actual de esa cantidad física utilizando un sensor de medición. Para regresar al set point, este 'error' debe minimizarse e idealmente debe hacerse igual a cero. Además, este proceso debe ocurrir tan pronto como sea posible. Idealmente, debería ser cero lag en la respuesta del sistema al cambio en su punto.
Más información puede encontrarse en muchos libros y Web incluidos aquí:
http://en.wikipedia.org/wiki/PID_controller
Implementación de PID
i) término de error (e):
Esto es igual a la diferencia entre el set point y el valor actual de la cantidad es controlada.
error = set_point – current_value (en nuestro caso es el error variable de la posición del Robot sobre la línea
II) término proporcional (P):
Este término es proporcional al error.
P = error
Este valor es responsable de la magnitud del cambio necesario en la cantidad física para alcanzar el punto de ajuste. El término de proporción es lo que determina el tiempo de subida del lazo de control o cómo rápidamente alcanzará el punto de ajuste.
III) término integral (I):
Este término es la suma de todos los valores de error anterior.
I = I + error
Este valor es responsable de la rapidez de respuesta del sistema al cambio desde el punto de ajuste. El término integral se utiliza el eliminar el error de estado estacionario requerido el término proporcional. Por lo general, pequeños Robots no utiliza el término integral ya no estamos preocupados por el error de estado estacionario y puede complicar el templar del lazo.
IV) término diferencial o derivado (D):
Este término es la diferencia entre el error instantáneo desde el punto de ajuste y el error desde el momento anterior.
D = error - previousError
Este valor es responsable de frenar la tasa de cambio de la cantidad física cuando se trata de cerca el punto de ajuste. El término derivado se utiliza reducir el sobrepaso o cuánto el sistema sobre corrige.
Ecuación:
PIDvalue = (Kp * P) + (Ki * I) + (Kd * D)
Donde:
KP es una constante, que se utiliza para variar la magnitud del cambio requerido para alcanzar el punto de ajuste.
Ki es la constante, que se utiliza para variar la velocidad en que el cambio se debe traer en la cantidad física para alcanzar el punto de ajuste.
KD es la constante, que se utiliza para variar la estabilidad del sistema.
Un enfoque es definir la variable Kd a 0 y poner a punto el término Kp solo primero. KP de 25 es un buen punto de partida en nuestro caso aquí. En el último paso hemos utilizado un Kp de 50 que funciona muy bien con mi Robot. Si el robot reacciona demasiado lentamente, aumente el valor. Si el robot parece reaccionar rápido y se vuelven inestables, disminuir el valor. Una vez que las respuestas del robot razonablemente, afinar la parte derivada del lazo de control. Primero establecer el Kp y Kd valor cada 1/2 del valor de Kp. Por ejemplo, si las respuestas del robot razonables con un Kp = 50, luego fije el Kp = 25 y Kd = 25 para empezar. Aumentar la ganancia de Kd (derivado) para disminuir el sobrepaso, disminuir si el robot se convierte en inestable.
Uno de los componentes del lazo a considerar es la velocidad real de la muestra/del lazo. Esta acelerando o desacelerando este puede hacer una diferencia significativa en el rendimiento del robot. Se establece por las declaraciones de delay que tiene en su código. Es un error tratar de metod provisional para obtener el resultado óptimo
Basado en el enfoque anterior, se implementó la siguiente función:
void calculatePID()
{
P = error;
I = I + error;
D = error-previousError;
PIDvalue = (Kp * P) + (Ki * I) + (Kd * D);
previousError = error;
}
La constante Kp simple utilizada en el último paso será reemplazada por este PIDvalue más completa:
void motorPIDcontrol()
{
int leftMotorSpeed = 1500 - iniMotorPower - PIDvalue;
int rightMotorSpeed = 1500 + iniMotorPower - PIDvalue;
leftServo.writeMicroseconds(leftMotorSpeed);
rightServo.writeMicroseconds(rightMotorSpeed);
}
Pero tenga en cuenta que si tienes Kd y Ki = 0, PIDvalue es sólo Kp * error como en el último paso












