Paso 6: ¿Qué es pi?
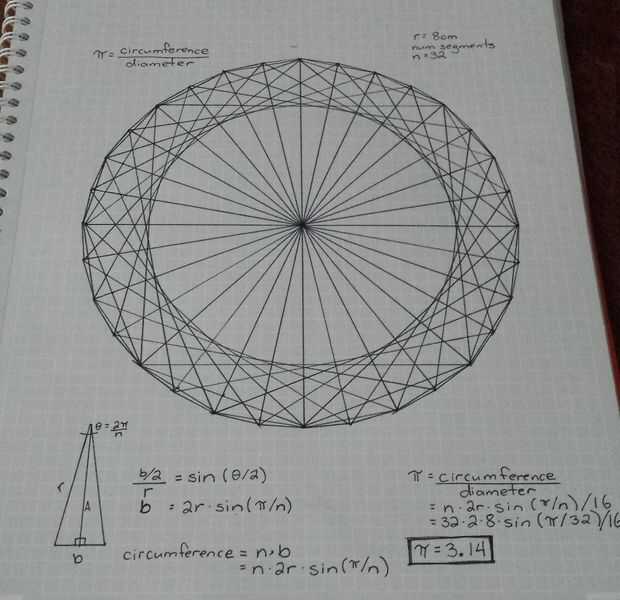
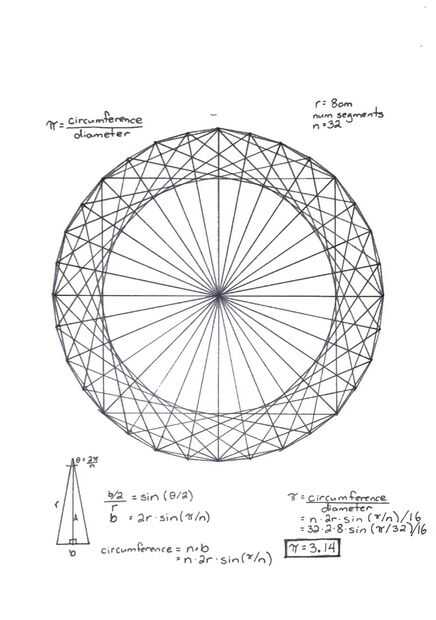
PI es dividida por el diámetro de la circunferencia. Sabemos el diámetro 16cm (para mí), así que ¿cuál es la circunferencia? Es la suma de todas las bases de los triángulos isósceles.
La base de un triángulo isósceles puede ser calculada usando la trigonometría (cierto es que algo no tenían Arquímedes, pero esto hace más fácil... Si quieres hacerlo como Arquímedes, utilice una regla).
Por lo tanto, sabemos que sin(angle/2) = (base/2) / radio y sabemos que el ángulo va a ser 2 * 360 ° / n, donde n es el número de triángulos en el círculo. Así que la base es: base = 2*radius*sin(360˚/n).
Ahora la circunferencia es n * base, que podemos ampliar como n*2*r*sin(360˚/n).
Así que vamos a encontrar pi n = 32.
PI = circunferencia/diámetro
PI = [n*2*r*sin(360˚/n)] / 16
PI = [32*2*8*sin(360˚/32)] / 16
PI = 3,14... Ta-da!
Mientras que esto no muestra realmente Arquímedes calculando pi (ya que sine funciones necesita pi) se muestra el uso de porciones infinitesimales para calcular los valores. Si lo hace el mismo cálculo en n = 4, obtendrá algo como pi = 2,83. Modo apagado, pero el más delgado (más infinitesimal) tus triángulos conseguir, más para pi get... y más su forma se parece a un círculo real!!!!!! Diversión!!!!!!