Paso 1: Teoría de la trayectoria
La presentación:
Hay dos cuerpos en movimiento en este proyecto. La primera es la bala (el mármol) y el segundo es el mono (u otro juguete de peluche). Un tirador voluntario está parado en un lado de la habitación y tira la canica sale del extremo del tubo de PVC como un spitball. En el otro extremo de la sala cuelga un peluche de un electroimán. Como el mármol cierra el extremo del tubo, se rompe un contacto pequeño alambre. Cuando el contacto del alambre se rompe, el electroimán se apaga, dejando caer el juguete. El mármol puede golpear el juguete cae cada vez, sin importar la velocidad de los rodamientos de bolas. Los estudiantes siempre se sorprenden por esto.
La teoría básica:
(Perdón por la longitud de esta explicación) En el plano 2D obviamente hay 2 direcciones: la x y la y. Por lo tanto, con el fin de describir con precisión la posición y el movimiento en el plano de un cuerpo, debe describir su posición x, la velocidad y aceleración, así como su posición y, velocidad y aceleración. Este experimento no se produce cuando los cuerpos están en equilibrio, será necesario también describir el cuerpo posición, velocidad y aceleración en diferentes tiempos. No te preocupes, no es solo tome complicado constante.
Ecuaciones de movimiento:
Si estás familiarizado con la física debe saber las ecuaciones de movimiento (con aceleración lineal constante):
Posición: s (t) = s0 + v0 * t + 1/2 * a * t ^ 2, donde s = posición (x o y), v = velocidad (x o y componente), a = aceleración (x o y componente)
Velocidad: v (t) = v0 + a * t
aceleración: se trata de 0 para direcciones horizontales o la aceleración debido a gravedad en direcciones verticales.
Utilizando las ecuaciones:
Tenemos dos cuerpos diferentes por lo que tendremos que mirar cada uno por separado.
Cuerpo 1, el mármol:
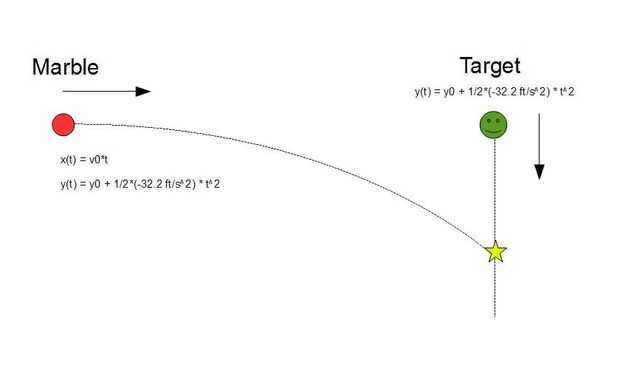
"Estado inicial" del mármol será el estado cuando se deja el extremo del cañón. Por lo tanto, tendrá sólo un componente de x de la velocidad inicial. Si descuidamos la resistencia del aire y la fricción, no tendrá un componente de x de accleration. Por lo tanto, la componente x de posición para el mármol se ve así: x (t) = x0 + v0 * t. Si asigna el sistema de coordenadas tal que la posición x inicial del mármol es cero (como en mi figura), la ecuación es simplemente x (t) = v0 * t. Puede utilizar una fotopuerta al final del cañón para obtener la velocidad exacta de la bala, o usted puede hacer para el bien de la ilustración.
Ya que queremos saber la hora y la posición de los dos cuerpos que chocan, y puesto que el mono está cayendo hacia abajo (no se cambia en x posición) que significa que queremos sabe la hora en que la posición x del mármol es igual a la posición x del mono. Tendrás que medir esta distancia cuando se configura en su aula. Supongamos que se mide para ser 25 pies y que el rodamiento se mueve a 50 pies por segundo. Esto es lo que la ecuación sería: 25 ft = 50 ft/s * t. resolver para t para conseguir que el mármol estará en las mismas coordenadas x como el mono en t = 0,5 segundos.
Cuerpo 2, el mono cae:
Ahora sabemos que cuando el mármol se llega y le golpeó al mono. Pero tenemos que saber donde estarán los dos en espacio vertical cuando chocan. Tomar la ecuación de la posición y para el mono: y (t) = y0 + v0 * t + 1/2 * a * t ^ 2. Ahora en este caso, y0 será altura inicial que el mono se cuelga en el, no tendrá una velocidad inicial y la aceleración es la aceleración debido a la gravedad. Por lo tanto, la ecuación se parece a esto: y (t) = y0 + 1/2 * (-32.2 ft/s ^ 2) * t ^ 2. Tenga en cuenta que si lo hizo la posición y la canica se acercaba con la misma ecuación exacta. Esto significa que siempre estarán en la misma posición y!
OK, así que nos dimos cuenta que llegará a t = 0,5 segundos así que vamos a enchufar que (asumiendo que la altura inicial del mono es de 6 pies del suelo):
y (t) = 6 pies + 1/2 * (-32.2 ft/s ^ 2) * (.5 seg) ^ 2. Problemas para la posición y obtenemos y = pies 1,975. TA daaa! La bala golpeará al mono después de medio segundo y 1,975 pies sobre el piso.
Para los estudiantes avanzados / educadores:
Usted puede hacer esto como complicado como usted quisiera. Pida a los estudiantes obtener las ecuaciones, o proponer un escenario con no constantes aceleraciones y velocidades (Nota: esto no garantiza que se golpean entre sí). Si saben calculo, ayudarlos a darse cuenta que las ecuaciones de movimiento son derivados unos de otros.













