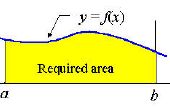
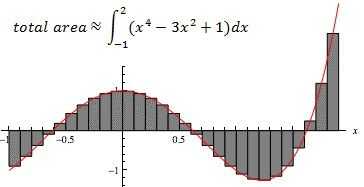
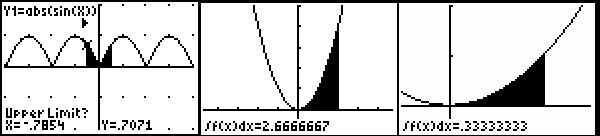
Paso 2: Sumas de Riemann
1. encontrar una función que (x, y) coordenadas se puede calcular sobre un intervalo. Intervalos comunes generalmente comienzan en o centro alrededor de x = 0.
2. dividir el área bajo la curva en razonablemente pequeños segmentos rectangulares de un ancho uniforme. Por ejemplo, 0,1 x unidades de distancia.
3. aproximado la altura de cada segmento con el valor y de la función a medio camino entre los valores de x alta y baja. En algunas circunstancias, usted puede específicamente una aproximación que es demasiado alta o demasiado baja, para utilizar un valor diferente y en el segmento de curva.
4. encontrar el área de cada segmento multiplicando altura por ancho. Usted tendrá que grabar estas áreas individuales para el siguiente paso.
5. añadir las áreas para encontrar el área total bajo la curva para el intervalo. Se trata de una gran cantidad de trabajo del matemático ronco, pero es confiable y casi se aproxima a la superficie total, sobre todo con más segmentos estrechos. Esto es cómo la mayoría de calculadoras realizan integrales.