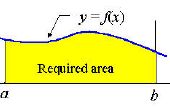
Paso 3: Integración definida
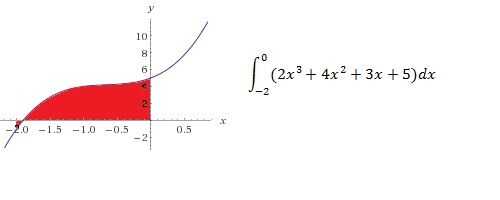
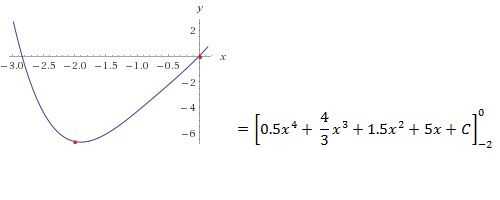
1. encontrar un polinomio simple, como en los pasos anteriores.
2. encontrar una regla de derivación que podría producir la función de. Ya que hay numerosos tipos de funciones y de infinitos ejemplos para cada tipo, así como combinaciones de tipos, junto con algunas funciones que son imposibles de integrar, exhaustivamente no puede explorar las opciones para la integración; en este caso, la respuesta debería ser simple.
3. revertir el proceso de derivación. Para un término polinomial, aumentar al exponente uno y dividir el coeficiente por el exponente de la nueva.
4. representan una constante de integración. Cuando encuentre la derivada de un polinomio que da y como una función de x, el término final, que está en el poder de x ^ 0, se pierde. Un derivado del polinomio dado puede provenir de un número infinito de polinomios de padres. Sin embargo, todas las coordenadas se cambian de puesto por la misma constante, por lo que el siguiente paso todavía funciona.
5. encontrar la diferencia entre los extremos de la función integrada de. Porque la función original, derivado de esta nueva función, da la serie de slops entre estos extremos, esta diferencia es igual al área bajo la curva de la función original. Esta relación es en gran medida intuitivo, así que trate de trabajar tantos ejemplos como sea necesario para observarlo.