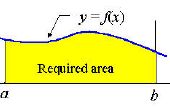
Paso 4: Aplicaciones físicas: avance aceleración y desaceleración
1. Imagine un coche que empieza en reposo, acelera durante 5 segundos a 2 ft/s ^ 2, entonces se ejecuta constantemente a 10 ft/s durante 5 segundos, luego disminuye a un ritmo de 1 ft/s ^ 2 hasta que se detenga.
2. tratar de encontrar la distancia desde el punto de partida mentalmente. Este debe ser ligeramente complicado, ya que la tasa de movimiento cambia con el tiempo. Las partes sólo fáciles para resolver mentalmente son la distancia recorrida a una velocidad constante y el tiempo que toma para detener (10-1t = 0, así t = 10). Puede verificar su respuesta a continuación, y después probar el método matemático.
3. el problema de la historia de la rotura en una función por trozos. La velocidad y el tiempo pueden ser representados como v = 2t para 0 a 5 t, v = 10 para 5 a 10 t y v = 20 t de 10 a 20 t.
4. integrar las piezas por separado con respecto a la variable t.
- v = 2t: el exponente debe ser un grado más alto y el coeficiente debe ser dividido por el nuevo exponente. Puesto que el exponente se implica uno, obtenemos x = t ^ 2 durante el intervalo t de 0 a 5. Esto da x = (5) ^ 2-(0) ^ 2 = 25.
- v = 10: la velocidad es constante, pero podemos utilizar este paso para comprobar que nuestro razonamiento es sonido. La regla de exponente da x = 10t, dado t de 5 a 10, que es x = 10 10-5 = 50.
- v = 20 t: integrar cada término por separado; x = 20t - 0.5t ^ 2 de 10 a 20, que es x=20(20) - 0.5 (20) ^ 2 - [20(10) - 0.5 (10) ^ 2] = 50.
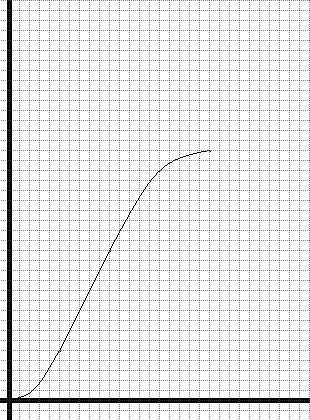
5. comparar la suma de las integrales al gráfico. Tenga en cuenta que la escala vertical es de 5 pies por cada bloque.