Paso 3: Compruebe los resultados: Cómo escribir su propia versión de cemento y probar para ver lo bien que funciona!



¿Cómo sabemos qué tan bien funciona el cemento?
Una manera de probarlo es tomar 3 fotografías de una escena o un objeto iluminada por luces de 2, como se muestra arriba (de nuestra ICIP2004 de papel; ver referencia al final del documento).
La primera imagen, llamada "v1.jpg", es una fotografía tomada con una luz encendida. Llamar a esa una lámpara de luz 1. En nuestro caso, que es la lámpara a la izquierda de nuestro espacio de estudio (Nótese cómo proyecta sombras a la derecha de sus correspondientes objetos).
La segunda imagen, llamada "v2.jpg", es una foto con la luz apagada y otra luz encendida, decir lámpara 2 encendido, por lo que v2 es la imagen, iluminada sólo por la lámpara 2. En nuestro caso, la lámpara 2 es el derecho de nuestro espacio de estudio (Nótese cómo proyecta sombras a la izquierda de sus correspondientes objetos).
El tercer cuadro, llamada "v3.jpg", es un cuadro con dos luces de encendido juntos. Observe cómo vemos dobles sombras en esta foto.
Ahora trate de v2 y v1 de cementación juntos, llame el resultado "v12.jpg".
Prueba ahora a ver cómo similares v12 es v3.
La forma más fácil de leer estas imágenes en una matriz es descargar las imágenes en raw:
http://wearcam.org/instructableCEMENT/octave_scrip...
http://wearcam.org/instructableCEMENT/octave_scrip...
http://wearcam.org/instructableCEMENT/octave_scrip...
pero si tienes una conexión de red lenta, simplemente coge las imágenes .jpeg y descomprimirlos:
djpeg-gris v1.jpg > v1.pgm
djpeg-gris v2.jpg > v2.pgm
djpeg-gris v3.jpg > v3.pgm
Editar hacia fuera de la cabecera para que tengas los datos en bruto, salvo, digamos, como archivos "v1", "v2" y "v3".
Usted puede hacer esto en Matlab, pero si estás en el verdadero espíritu DIY, prefiere utilizar el programa gratuito + opensource "octava": apt-get install octava y luego intente esto:
fid1=fopen('v1');
fid2=fopen('v2');
fid3=fopen('v3');
v1=fread(fid1,'uint8');
V1=Reshape(v1,2000,1312); estas dimensiones son suponiendo que haya descargado de wearcam %
V2=fread(fid2,'uint8');
V2=Reshape(V2,2000,1312);
V3=fread(fid3,'uint8');
V3=Reshape(V3,2000,1312);
colormap("Gray");
Image(v1/4);
Image(V2/4);
Image(V3/4);
V12 = v1 + v2;
e=SUM(SUM((V12-V3).^2))
Que devuelve:
e = 9.0995e + 09
Si descargaste desde Instructables, las dimensiones de la imagen pueden haber cambiado, por ejemplo, si las dimensiones son algo como 1024 por 672, cambiaran lo anterior cambiar la forma de comandos:
V1=Reshape(v1,1024,672);
y lo mismo para V2 y V3.
Nosotros sólo hemos cementado dos las dos imágenes de una lámpara en octava, sumando simplemente los y probadas para ver cómo similar son la imagen con ambas luces encendidas.
Ahora en lugar de añadirlos, trate de tomar la raíz cuadrada de la suma de sus cuadrados, es decir, como una medida de "distancia":
V12=sqrt(v1.^2+V2.^2);
e=SUM(SUM((V12-V3).^2))
y lo que tienes es un error mucho más baja:
ANS = 6.5563e + 08
Ahora, pruebe los cubos y tomando la raíz cúbica; Aquí el error es un poco más bajo todavía:
ANS = 2.2638e + 08
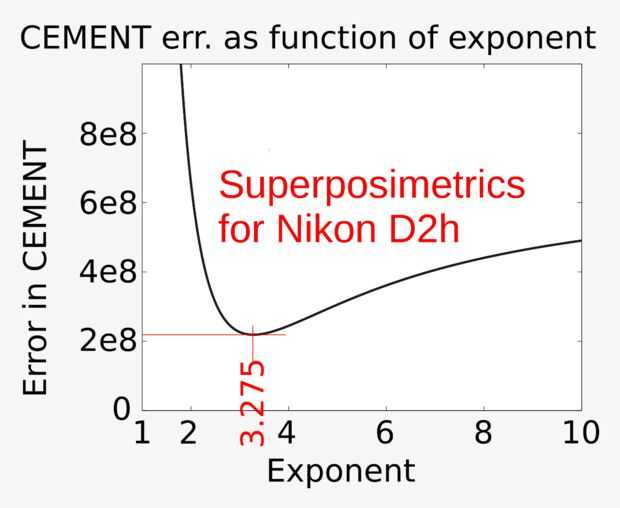
Más generalmente, podemos elevar a un exponente, n y luego tomar la raíz nth. Supuesto n no necesita ser necesariamente un número entero. Así que vamos a probar un montón de diferentes valores de "n" y una gráfica del error en función de "n". Esto lo podemos hacer bien por una función simple de la octava de la escritura en un archivo llamado "err.m":
función err=err(v1,v2,v3,N)
if(nargin~=4)
DISP ("err debe tener exactamente 4 argumentos de entrada: v1, v2, v3, n");
final % si
if(Max(Size(N))) > 1
DISP ("err sólo aborda vector N, no de arreglos de N");
final % si
por k=1:length(N)
n=N(k);
V12=(v1.^n+V2.^n).^(1../n);
ERR (k) = sum(sum((v12-v3). ^ 2));
% final para
Ahora podemos probar cemento para un montón de valores de "N" en una larga lista, por ejemplo, vamos a intentar 1000 diferentes valores de N va de 1 a 10:
N=(1:.01:10).';
El error para cada uno de estos es en:
e=ERR(v1,V2,V3,N);
que es un mínimo alrededor de 3,27 o 3.28 (cerca igual para esos valores de N), así que vamos a decir que el valor óptimo de "N" es 3.275.
El valor óptimo de "N" depende de la función de respuesta de una cámara especial, que en mi caso la Nikon D2h.
Otros que han hecho estos valores Informe Instructable "N" para otras cámaras, por lo que propongo la creación de un enorme Superposimetric "tabla" como la "La gran carta de Dev" para la película:
Tabla de Superposimetric masiva:
Cámara hace y el modelo de función de la respuesta número "n"
Nikon D2H 3.275
Nikon D60 3.3
SONY RX100 2.16
Canon Powershot S50 2.1875
Yendo más lejos:
Hemos utilizado una ley simple poder aquí para fines ilustrativos, pero de hecho, podemos hacer algo mucho más poderoso: realmente podemos desbloquear los secretos de cualquier cámara, de forma no paramétrica, es decir, determinan su función verdadera respuesta, de tres cuadros, como la anterior, pero en vez de solucionar para una "n" Resolvemos para las 256 entradas de la función de respuesta de cámara quantimetric. Véase, por ejemplo: